11

- Necessità di una rinnovata riflessione sul problema dell’ordine
- L’idea di un ordine intrinseco
- Ordine e ripetizione
- Ripetizione semplice e ripetizione concatenata
- Ordine intrinseco e concatenazione

Abbiamo tuttavia attirato l’attenzione sul fatto che una stabilità fattuale - sia che dipenda dalla conformazione fisica della cosa stessa sia da qualche consuetudine consolidata (come nell’esempio degli amici del bambino che abbiamo rammentato in precedenza) - è ancora lontana dal poter proporre il pensiero del numero. |2|

L’insegnamento che possiamo trarre dalle considerazioni svolte fin qui è che questo pensiero è vincolato ad un ordinamento che sia tale per ragioni essenziali, il che significa ad un ordinamento necessario, a priori. Non abbiamo nessuna difficoltà ad impiegare vecchie parole della tradizione filosofica, ma vorremmo farlo determinandone con chiarezza il contesto. |3|

Cosicché ci chiediamo: che tipo di connessione deve sussistere tra un elemento e l’elemento successivo di una successione affinché si possa parlare di un ordine intrinseco, che sia del tutto indipendente da considerazioni empirico-fattuali? Quale condizione deve essere soddisfatta affinché un determinato elemento di una successione occupi necessariamente e non occasionalmente una determinata posizione? |4|

Per rispondere a questa domande in realtà dobbiamo spostare la nostra attenzione proprio, e finalmente, al problema della ripetizione. Ad esso dobbiamo ripensare tenendo conto di ciò che abbiamo già detto, ma anche del nuovo contesto in cui il problema ci si ripresenta, che non può dare per acquisito, come potevamo invece fare in precedenza, la nozione del numero. Potremmo allora, rispettando questa consegna, richiamarci non tanto all’idea della molteplicità e degli oggetti di cui essa è costituita quanto piuttosto all’esercizio di un’azione ovvero all’esecuzione di un’operazione. Soprattutto in rapporto ad azioni o ad operazioni si parla di ripetizione. Oppure in rapporto ad eventi, i quali peraltro sono in via di principio all’interno di una processualità. Quando questo termine viene riferito ad oggetti viene implicata, più o meno debolmente, una componente dinamico-processuale, sia in quanto si tratta di oggetti che fanno effettivamente parte di eventi (come nel caso di suoni all’interno di una melodia), sia attraverso una «proiezione» che conferisce un dinamismo interno alla staticità dell’oggetto. |5|

Quest’ultimo caso è per noi particolarmente interessante: talvolta possiamo trovare opportuno parlare di ripetizione in rapporto ad una configurazione visiva, ad esempio potremmo usare questo termine in rapporto ad una configurazione come la seguente: |6|

Questa è una circostanza interessante perché il vedere nella figura qualcosa che si ripete significa in certo modo proiettare l’ordine della figura sul piano di una operazione possibile che la ha generata:

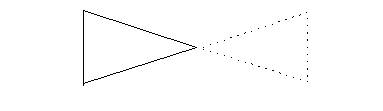
Se in questo caso parliamo di ripetizione, potremmo osservare che con questa parola si fa emergere un’allusione, ad esempio, ad una possibile operazione di duplicazione e di rotazione a specchio: la figura così intesa viene riarticolata e questa riarticolazione viene interpretata riportandola ad una procedura da cui essa potrebbe essere stata generata. |7|

Si riporta l’ordine alla ripetizione. L’ordine appare come un risultato, come qualcosa che è stato prodotto, e dietro l’oggetto si intravvede un modo di realizzazione possibile della figura. |8|

Un fascio di relazioni molto ricco e complesso collega ordine e ripetizione. Ma vi è un caso semplice che mostra esemplarmente, e in modo particolarmente forte, questo rapporto considerando unicamente la nozione dell’operazione ripetuta. |9|

Dobbiamo notare anzitutto che ci sono almeno due modi di considerare la ripetizione di un’operazione. |10|

Un modo è quello che potremmo chiamare la ripetizione semplice. Supponiamo ad esempio che un maestro proponga alla lavagna un triangolo e chieda agli allievi di ricopiarlo. Potrebbe in particolare chiedere che questa azione venga ripetuta più volte. Poiché non vi sono altre istruzioni, gli allievi potranno disegnare triangoli in qualunque parte del foglio, e in qualunque disposizione. Quindi: disordinatamente. |11|

Certamente i triangoli vengono disegnati l’uno dopo l’altro e quindi vi è un ordine temporale della successione, ma di questo non rimane traccia sul foglio di carta e non è leggibile in esso. In certo senso esso è un ordine meramente soggettivo perché riguarda riguarda le azioni come tali e non il loro prodotto. |12|

Ogni passo è chiuso in se stesso nel senso che non presuppone né l’azione precedente né quella successiva. L’oggetto prodotto potrà di conseguenza essere considerato come un oggetto a sé stante, eventualmente con relazioni di somiglianza con gli oggetti che gli stanno intorno. |13|

Diversamente stanno le cose per quella che potremmo chiamare ripetizione concatenata. |14|

Se ad esempio, l’istruzione fosse quella di copiare il modello più volte allineando i triangoli tra loro, in base a questa condizione aggiuntiva cominceremmo ad uscire dalla semplice ripetizione per il fatto che dovremmo appunto «agganciare» ciascun disegno al disegno precedente, e l’ordine non avrebbe più carattere meramente temporale ma si imprimerebbe nel disegno che assumerebbe anche, in forza di esso, un carattere ad un tempo dinamico ed unitario. Gli oggetti prodotti non saranno semplicemente a sé stanti, ma apparterebbero ad un’unità più ampia che si va dispiegando con la ripetizione. |15|

La condizione potrebbe essere rafforzata - ad esempio stabilendo che ad ogni passo, a partire dal modello, il triangolo deve essere rappresentato ruotato a destra di 90°.

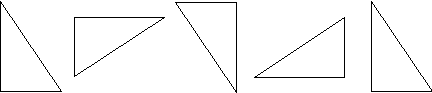
In questo caso non si può prescindere anzitutto dalla disposizione del triangolo dato come modello e ogni figura risulta fortemente concatenata alla figura precedente ed alla figura successiva. La figura fornita come modello dal maestro assume nettamente il carattere di «inizio» di una successione di figure fra loro correlate. Alla terza ripetizione dell’operazione corrisponderà una disposizione determinata tra le quattro possibili disposizioni che il triangolo può assumere. |16|

Ogni passo è aperto al successivo e nello stesso tempo si ricollega al passo precedente. Il prima e il poi diventano irrilevanti per qualificare un’ordine che si trova ormai all’interno della serie di figure ed in dipendenza del tipo di operazione che le ha prodotte. |17|

Vogliamo ora considerare la nozione di operazione in un’astratta generalità: in essa si distinguerà la base dell’operazione, che è ciò su cui essa viene esercitata, e il risultato dell’operazione, che è ciò che viene prodotto nell’applicazione dell’operazione ad una base. Nella possibilità di fare del risultato di un’applicazione dell’operazione la base per una nuova applicazione di essa sta tutto il concetto della ripetizione concatenata. In rapporto ad essa parleremo anche di ripetizione (iterazione) ricorsiva o di ricorsione (restringendo dunque il termine di «ricorrere», che è un possibile sinonimo di «ripetere» o «iterare»). Occorre tuttavia notare che quest’ultima espressione - che appartiene ad un’elaborazione matematica evoluta - andrà sempre intesa in stretta aderenza al nostro contesto elementare di discorso[1]. |18|

Quando si verifica l’applicazione ricorsiva di un’operazione, a partire da un unico oggetto inteso come inizio, il risultato complessivo, ottenuto in un punto qualunque dell’applicazione, sarà una successione di elementi attraversata da un ordine intrinseco. In effetti, essendo dato un primo elemento, ogni altro elemento è costruito in modo da presupporre, nella regola della sua costruzione, l’elemento precedente. |19|

In questo contesto, le vecchie parole della nostra tradizione filosofica come essenziale, necessario, a priori assumono un significato pienamente comprensibile. |20|

L’interruzione della ricorsione dovrà, a sua volta, essere ritenuta puramente «accidentale». In altri termini non vi sono ragioni di principio perché l’applicazione ricorsiva debba terminare in questo o quel punto - cosicché possiamo dire che l’iterabilità spetta all’operazione in via di principio, e ciò significa naturalmente la stessa cosa che affermare che essa è iterabile ad infinitum. |21|

È interessante notare che, come in precedenza il tipo di relazione tra gli elementi del corpo non consentivano la «proseguibilità» della serie, così ora questa proseguibilità è garantita ed assicurata dalla stessa idea della concatenazione. La relazione che sussiste tra un elemento della serie e l’elemento precedente assicura che dato un elemento se ne potrà sempre costruire un altro. Si è messa in moto una macchina inarrestabile. Questa apertura infinitaria fa parte della rete concettuale che siamo riusciti a fare emergere liberandoci dalle scorie delle nostre precedenti esemplificazioni empirico-concrete. |22|

§ 10

§ 12