8
- Introduzione nel simbolismo dei segni che indicano il mutamento di direzione
- Esempi di calcoli

Si tratta di vedere se di un simile risultato, che in se stesso potrebbe sembrare alquanto peregrino, possiamo realmente farcene qualcosa. Abbiamo forse fatto qualche guadagno significativo nel porre le cose in questo modo? È realmente interessante assumere un punto di vista che già in rapporto ad una figura così elementare richiami l’attenzione sulla possibile presenza del tema della ripetizione? Che importanza e che peso dobbiamo dare al passaggio ad una scrittura simbolica come quella che è stata or ora proposta? Intanto, per cominciare a dare una risposta a partire da quest’ultima domanda, questo simbolismo ci aiuta a pensare, attraverso di esso la nostra riflessione successiva può trovare un nuovo orientamento ed una nuova direzione. Abbiamo solo bisogno di comprendere in che modo esso possa essere reso un poco più complesso - esso è realmente troppo elementare - e in che modo potremmo impiegarlo eventualmente introducendo di volta in volta tutte le modificazioni che riterremo utili ai nostri scopi. |2|

Per compiere un primo passo: la successione dei tratti, nel caso precedente, si sviluppa in un’una unica direzione. Si potrebbe allora proporre come primo arricchimento, oltre il segno F, un segno che indichi il cambiamento di direzione verso destra ed un segno che indichi il cambiamento di direzione verso sinistra secondo un angolo la cui grandezza potrà essere di volta in volta prefissata. |3|

Per indicare il mutamento di direzione verso sinistra scegliamo il segno « + », per indicare il mutamento di direzione verso destra scegliamo il segno « - » , segni che non avranno dunque in questo contesto alcun significato aritmetico, e che ovviamente potrebbero essere sostituiti da qualunque altro. Il nostro linguaggio si arricchisce di due segni e di una condizione. I segni sono il «+» e il «-». La condizione è la grandezza dell’angolo. |4|

Il percorso diventa così più mosso, potremo ottenere una grande varietà di linee, ed in particolare queste linee potranno essere chiuse ed anzi dar luogo ad alcune figure geometriche che ci sono familiari. |5|

Supponiamo ad esempio di fissare la condizione di un angolo di 120° e di scrivere la sequenza di segni:

F+F+F

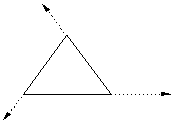
Occorre intanto attirare l’attenzione sul fatto che, essendo il mutamento di direzione inteso come deviazione da una direzione rettilinea da intendere come procedente da sinistra a destra, la grandezza dell’angolo deve essere misurata a partire da essa. |6|

F+F

Precisato questo punto è chiaro che la sequenza F+F+F può essere considerata un sostituto simbolico-notazionale di un triangolo equilatero. |7|

F+F+F

Quella sequenza può essere considerata come ottenibile a sua volta all’interno del seguente calcolo:

condizione: Angolo 120°

Inizio: x

Regola : x-> F+x

che dà luogo alla sequenza: F+x, F+F+x, F+F+F+x, ecc. La figura triangolare è ottenuta alla terza iterazione: al terzo passo la linea si chiude e verrà ripetuto esattamente lo stesso percorso. Andare oltre non ha dunque alcun interesse. Al terzo passo la stringa ottenuta è F+F+F+x che differisce dalla precedente F+F+F solo per il segno «+x», che è irrilevante rispetto alla sua interpretazione figurale; tuttavia questa differenza segnala sul piano della formula la novità nel concetto di figura a cui abbiamo già accennato[1]. |8|

Non vi è certo bisogno di spiegare che con un angolo di 90° si otterrà un quadrato, esattamente dunque con la stessa regola del triangolo, e con la sola differenza che le iterazioni dovranno essere quattro per ottenere la chiusura della figura.

Ed esattamente con la stessa regola, si potranno in generale formare figure regolari con tutti gli angoli che siano divisori di 360. Il numero dei lati sarà dato dal rapporto tra 360 e la grandezza dell’angolo, e sarà pari al numero delle iterazioni. |9|

Naturalmente con suddivisioni approssimate potremo costruire poligoni con lati sempre più brevi e infine, in rapporto alla realizzazione grafica concreta, indistinguibili dal cerchio. Nel caso seguente, lo stesso algoritmo genera, con un angolo pari a 10° alla 36a iterazione qualcosa di molto simile, dal punto di vista grafico, ad un cerchio:

E non siamo forse subito stimolati ad interrogarci che cosa accadrebbe se assumessimo che il tratto di base, in luogo di rimanere costante, crescesse per incrementi a loro volta progressivamente crescenti? |10|

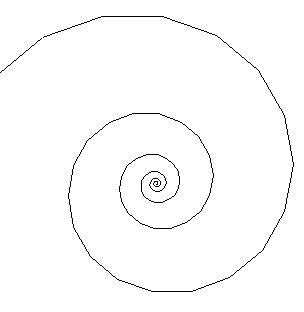
Per ottenere questa sequenza spiraliforme di tratti è ovviamente necessario introdurre una modificazione delle condizioni e delle regole costruttive: in particolare bisogna stabilire l’incremento e fare in modo che questo incremento sia cumulativo e che quindi porti ad un progressivo allungamento del tratto. |11|

Cominciamo ora a sospettare che possa verificarsi, attraverso variazioni introdotte nell’algoritmo, un’autentica esplosione di forme. Ma prima che ciò accada conviene indugiare in qualche parola di commento. Anzitutto già a questo punto del nostro tragitto ci sembra di poter dire che, a partire da una modificazione sul modo di concepire la linea, abbiamo mostrato la possibilità di «riunire sotto un unico concetto» una molteplicità assai varia di figure - confermando un pensiero che è già in precedenza affiorato, e cioè che la «subordinazione concettuale» non è affatto sempre e necessariamente da concepire come una unificazione tra cose che hanno proprietà comuni. Qui in effetti l’unità «concettuale» è costituita dal riferimento all’algoritmo, dalle regole e dalle condizioni che rappresentano nel loro insieme lo schema operazionale della costruzione - potremmo addirittura dire: il concetto è dato proprio da questo schema operazionale. E tanto più sembra opportuno mettere l’accento sulla terminologia del concetto, per il fatto che è proprio la concezione della figura che cambia, nella stessa misura in cui cambia il punto di vista da cui essa viene considerata, e variano dunque le nozioni a partire dalle quali essa viene pensata. |12|

Occorre qui attirare l’attenzione sul fatto che quel prospettivismo di cui tanto si parla nella fenomenologia della percezione in realtà può essere ampiamente esteso anche all’ambito delle formazioni intellettuali. Non vi è affatto il concetto del cerchio o il concetto della spirale, con la loro definizione logicamente in ordine che si pretende valga come definizione assoluta, ma modi prospetticamente diversi di intendere queste forme (di pensarle) che si rispecchiano nella molteplicità delle loro possibili «definizioni». L’elemento prospettico, che nella percezione è dato dalla differenza del luogo di osservazione, è qui fornito invece dalla differenza delle nozioni di riferimento. Forse si può sostenere che proprio l’ambito del pensiero matematico, che talora viene presentato come modello di univocità, si presenta invece come un campo interamente dominato da una pronunciata plurivocità prospettica. Non vi è forse in questo campo alcun concetto che se ne stia, per così dire, fermo in un preciso luogo, ma ognuno può essere colto secondo angolature diverse, secondo inclinazioni differenti. |13|

Annotazione –

Il linguaggio informatico a cui qui e nel seguito faccio ampio ed esplicito riferimento, è un linguaggio che appartiene alla tipologia degli L-systems ovvero «string rewriting systems». La prima idea di un sistema di produzione grafica attraverso la "riscrittura" di stringhe è dovuta ad Aristid Lindenmayer (1968). Si parla perciò anche di linguaggi di Lindenmayer e la lettera L richiama naturalmente questo nome. Essa è stata poi ripresa da A. R. Smith nel 1984 e da P. Prunsinkiewic nel 1986 (Graphical Applications of L-systems, Vision Interface, 1986, pp. 247-253) e dallo stesso Lindenmayer e Prunsinkiewic con diverse pubblicazioni e in particolare con il volume di P. Prusinkiewicz and A. Lindenmayer, The Algorithmic Beauty of Plants, Springer-Verlag, New York, 1990. Un breve schizzo sulla struttura degli L-systems è stato realizzato da Dietmar Saupe nella Appendice C (A unified approach to fractal curves and plants) nel volume da lui curato insieme a H. Peitgen The Science of Fractal Images, Springer Verlag, New York 1988. Tale linguaggio è a sua volta ispirato al linguaggio di programmazione Logo che fa parte della famiglia dei linguaggi Lisp. Quanto lontano si possa andare cominciando da un inizio tanto semplice è mostrato dal volume di H. Abelson e di A. Disessa, Turtle Geometry, MIT, 1980, trad. it. La geometria della tartaruga, Muzzio Editore, Padova, 1986. Tuttavia vi sono ragioni che andrebbero esaminate a fondo per le quali, nonostante la notorietà del problema, e l’ampiezza di direzioni il cui questa tematica può essere sviluppata e che è dimostrata da una bibliografia ormai molto ricca, essa non si è incontrata in modo significativo, che io sappia, con la riflessione epistemologica. In particolare non conosco nessuno scritto che si avvalga del riferimento agli L-systems in un contesto filosofico come quello qui proposto. Naturalmente ciò non significa che fin dall’inizio L-systems non fosse motivato da interessi scientifici e teorici molto forti: essi erano tuttavia orientati soprattutto in direzione delle tematiche della rappresentazione dei processi di crescita biologica e dei sistemi dinamici. Un parte non irrilevante dell’interesse è stata volta - come nel caso dei frattali in genere - all’ambito della computer graphics. Mi sembra necessario richiamare l’attenzione anche sulla rilevanza di questo genere di studi dal punto di vista epistemologico, ponendo in realtà questa rivendicazione in un quadro più generale: la riflessione epistemologica in genere non si è incontrata in modo realmente approfondito con le tecniche informatiche, da cui essa potrebbe attingere probabilmente molte idee, e inversamente da parte informatica forse non si è consapevoli delle implicazioni di ordine filosofico che si trovano all’interno di quelle tecniche, che non sono affatto puri marchingegni al servizio del calcolatore.

Per ciò che riguarda un possibile linguaggio L-system utile ai nostri scopi immediati, non è difficile realizzarne un’implementazione all’interno di un qualunque linguaggio di programmazione.

Si tratta fondamentalmente di realizzare un programma che consta di tre parti: dobbiamo infatti poter disporre di

(1) una procedura P₁ che, attraverso l’applicazione ricorsiva delle regole e delle condizioni ad una stringa iniziale, pervenga ad una stringa finale S₁;

(2) una procedura P₂ che interpreti ciascuna lettera di cui è composta S₁ e la converta in modo opportuno formando una matrice o una lista S₂ contenente le coordinate di schermo corrispondenti al percorso «cifrato» in S₁;

(3) una procedura P₃ che esegua su video il tracciamento delle linee in conformità a S₂.

Il linguaggio di cui fa uso Mathematica della Wolfram Research, che tratta splendidamente le stringhe e le liste, mi ha consentito la realizzazione di un linguaggio di questo tipo estremamente duttile, facilitando anche il dimensionamento a schermo con gli automatismi di rappresentazione grafica che sono propri di questo linguaggio. La maggior parte dei disegni di questo libro sono stati compiuti attraverso di esso. All’interno di un corso universitario sul tema della ripetizione tenuto presso l’Università di Milano nel 1994 - corso che sta all’origine di questo lavoro - ho realizzato esempi attraverso un’implementazione in Visual Basic. Programmi che realizzano istruzioni L-systems sono in ogni caso abbastanza numerosi e facilmente reperibili.

§ 7

§ 9