12

- La «crisi dell’intuizione» secondo Hans Hahn
- Discussione critica

Esso si intitola La crisi dell’intuizione [1] ed il suo scopo è quello di mostrare, sulla base di alcuni esempi tratti dall’ambito geometrico che la geometria, in tutte le sue possibili varietà, è una pura costruzione logica con la quale la cosiddetta intuizione ha ben poco da spartire, ed anzi rappresenta un freno ed un impedimento del pensiero. Non staremo qui a discutere gli scarsi cenni dedicati a Kant con cui si apre il saggio, per andare direttamente a due degli esempi fondamentali riportati da Hahn per sostenere la propria tesi in modo da dare a questa discussione la forma di uno sviluppo e di un consolidamento di quanto abbiamo or ora sostenuto. |2|

Il primo di essi riguarda la possibilità di funzioni continue, e tuttavia non derivabili in tutti i loro punti. È interessante intanto notare che questo stesso esempio ricorre in Poincaré, Il valore della scienza[2], e quindi in un autore che fa un suo discorso molto articolato sull’intuizione, e piuttosto propenso, come si sa, a valorizzarla. Di fatto tuttavia su questo esempio l’accordo tra Poincaré e Hahn è completo. Infatti esso viene proposto da Poincaré nel momento in cui egli vuole mostrare i limiti dell’intuizione e la necessità che i risultati ottenuti per via intuitiva vengano corretti ed eventualmente migliorati e resi sicuri dalla logica. In realtà anche l’opposizione stabilita da Poincaré tra logica e intuizione ci lascia del tutto insoddisfatti, ma naturalmente converrà limitarci qui alla questione particolare. Ecco quanto scrive Poincaré: |3|

«L’intuizione non può darci né il rigore né la certezza: ce ne siamo accorti sempre di più. Citiamo alcuni esempi. Sappiamo che esistono funzioni continue prive di derivate. Niente di più contrario per l’intuizione di questa proposizione che ci viene imposta dalla logica. I nostri padri non avrebbero fatto a meno di dire: ’E evidente che ogni funzione continua ha una derivata, poiché ogni curva ha una tangente’. - Come può l’intuizione ingannarci a questo punto?». |4|

Poincaré dà a questa domanda una risposta nettamente psicologizzante: ci raffigureremmo mentalmente una curva, come una linea senza spessore «ed allora è chiaro che potremo sempre rappresentarci questi due nastri sottili, l’uno rettilineo, l’altro curvilineo, in una posizione tale che si sfiorino leggermente senza attraversarsi. Saremo così condotti, a meno che un’analisi rigorosa non ci avverta, a concludere che una curva ha sempre una tangente»[3]. |5|

Vediamo ora come si articola la discussione di Hahn su questo punto. Anzitutto vi è il richiamo ai fondamenti del calcolo differenziale - e quindi al problema del movimento di un punto in un determinato istante ed a quello leibniziano della tangente. |6|

È chiaro, dice Hahn, che per l’intuizione un punto in movimento deve avere una velocità determinata in un determinato istante. E parallelamente deve essere intuitivamente evidente che una curva deve avere un’inclinazione determinata per ogni suo punto o almeno per la maggior parte di essi. |7|

Ora intanto è il caso di chiedersi, come prima domanda per così dire preparatoria: che cosa mai significa «intuizione» in queste formulazioni? È assai difficile dare una risposta. |8|

Evocando il calcolo differenziale ci si appella ad un altissimo livello di elaborazione teorica: in particolare l’idea del movimento del punto in un determinato istante è un’idea astratta che non fa parte affatto del concetto comune (quotidiano) di movimento (se si vuole intendere con intuizione qualcosa di simile ad un concetto comune). Forse il pensiero «quotidiano» può arrivare a concepire senza troppa difficoltà e con qualche spiegazione l’idea di velocità media. Il passaggio al limite invece richiede difficili spiegazioni, e deve essere teorizzato a fondo. Perché mai all’interno di questa complessa elaborazione teorica sarebbe proprio l’intuizione - questa pretesa facoltà intorno alla quale si sa ben poco - a suggerire erroneamente che ogni punto in movimento debba avere una velocità determinata in un determinato punto? Sembra assai più sensato sostenere che una simile posizione sia una conseguenza di un orientamento intellettuale complessivo e di una concezione dell’analisi nella quale determinati modelli abbiano un carattere normativo e dominante. Forse ciò che crea qualche problema non è l’intuizione (ammesso un qualche impiego sensato del termine), ma il tipo di matematica utilizzata e in particolare, l’esemplarità attribuita a certe forme funzionali piuttosto che ad altre. |9|

Attiriamo intanto l’attenzione su questa differenza: nella misura in cui si considera l’invenzione del calcolo infinitesimale come motivato, ad esempio, dal problema del movimento si riconosce già che l’intuizione ha una sua parte, in quanto si pensa alla dimensione reale del movimento, e non ad una questione puramente matematica. |10|

Quando si pone il problema di una curva continua senza derivate si ha di mira invece una questione puramente matematica - e quindi qualcosa che non può essere posto sullo stesso piano delle considerazioni relative al movimento. Come nessuno penserebbe di fare una passeggiata su una curva di Koch, così nessuno progetterebbe di costruire un autodromo che abbia come percorso la curva di Weierstrass. È tempo di dire a chiare lettere che l’intuizione - intesa come senso comune, o qualcosa di simile - non ha nessuna opinione sulla curva senza derivate: non sa nemmeno che cosa sia una derivata, anzi, a dire il vero, ha qualche difficoltà a capire che cosa si intenda con «curva» nella matematica in genere. |11|

Se in rapporto a questo tipo di problemi qualcosa viene trovato evidente o non evidente, ciò è appunto una questione che riguarda i «nostri padri» - come dice Poincaré: ed è assai ben detto. Infatti se le curve senza derivate dànno dei problemi, non li dànno all’intuizione, ma ai matematici; e ciò che viene messo in questione non è affatto la loro personale intuizione (come dire, la loro capacità immaginativa o cose di questo genere), ma proprio la matematica che hanno praticato fino a quel momento nella quale determinati modelli erano prevalenti. |12|

Mettere in questione il movimento è poi sbagliato anche per un’altra ragione: una volta che si è mostrato che esistono curve continue senza derivate, non si è dimostrato nulla intorno al movimento. Non vi è affatto un rapporto semplice tra l’una e l’altra cosa. |13|

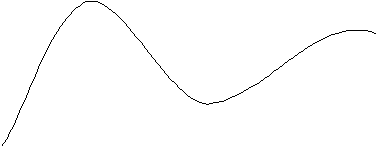
Analogamente per quanto riguarda il riferimento geometrico. In quanto si assume come modello di curva qualcosa di simile a questo:

naturalmente saremo portati a ritenere in linea generale che caratteristica eminente di una curva sia la possibilità di tangenti in ogni suo punto - ma non per il fatto che l’intuizione ci inganna e ci seduce, ma per il fatto che abbiamo scelto come modello proprio questo, e non un’altro. Abbiamo deciso cioè che la nostra geometria, ed in particolare nel momento in cui essa si è incontrata con il concetto di funzione, si sarebbe occupata prevalentemente di curve di questo tipo. Naturalmente non si trattò per nulla di una decisione arbitraria, ma dipendente dai problemi che avevano determinato quell’incontro. |14|

Se poi con intuizione intendiamo il riferimento a modelli percettivi, è chiaro che essa non contiene raccomandazioni particolari per il matematico - non raccomanda un modello piuttosto che un’altro. |15|

Dal punto di vista percettivo assumono rilievo due tipi con andamenti caratteristici nettamente differenti: un tipo come il precedente, che anche nel linguaggio corrente si chiama «curva», e un tipo come il seguente

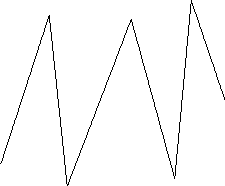
che invece il linguaggio corrente non chiamerebbe affatto «curva». Per la percezione siamo qui alla presenza di configurazioni tipicamente differenti, e persino contrapposte, e di cui viene valorizzata proprio la contrapposizione; mentre il pensiero astratto tenderà a riunirle possibilmente sotto un unico titolo. |16|

Ora, è il pensiero astratto che fa della prima un modello per la seconda piuttosto che l’inverso. L’intuizione come tale in questa faccenda non c’entra per nulla. |17|

E riguarda ancora soltanto il pensiero astratto il fatto che il secondo tipo di curva non sia dominabile mediante gli strumenti analitici correnti. |18|

Fatte queste premesse, vogliamo vedere più da vicino almeno i due primi esempi recati da Hahn, che ci interessano direttamente per ragioni che appariranno subito chiare. |19|

Il primo di questi esempi è la curva priva di tangenti in ogni suo punto escogitata da Weierstrass nel 1861. «Si era soliti pensare - commenta Hahn [4] - che l’intuizione ci obbligherebbe a riconoscere che una simile deficienza [la mancanza di tangenti] potrebbe verificarsi solo in punti isolati ed eccezionali di una curva e non in tutti i suoi punti. Si credeva che una curva dovesse possedere una inclinazione esatta, ovvero una tangente, se non in ogni punto, almeno nella netta maggioranza di essi». |20|

La circostanza curiosa è che Hahn inizia la propria esposizione osservando che di una simile curva senza tangenti si può dare una dimostrazione con un’illustrazione intuitiva relativamente semplice [5] . Si tratta di un’osservazione del tutto giusta. Egli ne dà infatti una descrizione evitando l’«intricato e arduo calcolo» con il quale Weierstrass perviene ad essa. In realtà si può fare di più e di meglio: è possibile evitare di ripetere la descrizione di Hahn, riprendendone tuttavia alcuni aspetti essenziali, e presentare invece, dopo averci pensato un poco sopra, la sua definizione operazionale, ovvero lo schema attraverso cui la curva può essere generata. |21|

Infatti la curva di Weierstrass è una «spezzata» generabile all’interno di un algoritmo ricorsivo non troppo dissimile dalla nostra curva di Koch. Dovremo tuttavia, per raggiungere lo scopo, adattare nuovamente il linguaggio L-system introducendo due segni A e B che saranno interpretati graficamente nello stesso modo di F: entrambi indicheranno dunque un tratto, con la sola differenza che A indicherà un tratto ascendente e B un tratto discendente, secondo un angolo prefissato che rimarrà costante[6]. |22|

In effetti l’assioma sarà semplicemente rappresentato da un tratto ascendente e da un tratto discendente, mentre le due figure corrispondenti alle regole di sostituzione per A e per B e destinata ognuna a sostituire un tratto ascendente ed un tratto discendente, saranno l’una il «rovescio» dell’altra.

   

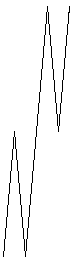
La formula della curva di Weiestrass risulta allora essere la seguente, assumendo come condizione un angolo a 85°. |18|

Sulla base di questo schema avremo alla prima ed alla seconda iterazione le figure seguenti:

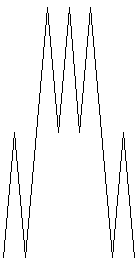
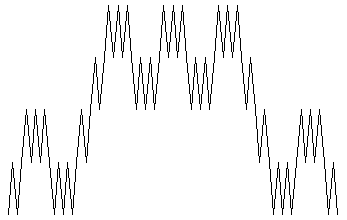
A questo punto non possiamo far altro che ripetere un commento che abbiamo già fatto in precedenza. Dallo schema operazionale, dal calcolo e dai primi risultati figurali corrispondenti si comprende con evidenza che nel corso delle iterazioni gli «spigoli» si andranno sempre più infittendo. Sulla base del passaggio infinitario, reso possibile dal pensiero dell’ecceterabilità del processo, sarà poi possibile parlare di un simile curva come di una curva priva di tangenti in tutti i suoi punti. |19|

Dove è allora la crisi dell’intuizione? È chiaro che il passaggio infinitario pone questo «oggetto» su un piano interamente astratto, facendo di esso un oggetto puramente intellettuale: considerato in quanto tale, esso non ha nulla di intuitivo, ma questa è una scoperta degna soltanto di Monsieur de Lapalisse. Se qui vi è qualche problema, e certamente vi è, si dovrà trattare di un problema interno al pensiero matematico, ai suoi metodi ed agli strumenti intellettuali che esso mette in campo; le eventuali difficoltà non provengono da qualcosa che stia al di fuori della matematica e che le sia estraneo e persino ostile. Se i padri della matematica di una volta ritenevano impossibile un oggetto simile avevano le loro buone ragioni - questo oggetto «infinito» non è certo un oggetto qualunque (è anzi un oggetto un po’ strano - come si lascia sfuggire Hahn). E le ragioni più importanti di questo loro atteggiamento non erano affatto, io credo, di ordine meramente «psicologico», come sempre viene suggerito in contesti come questi. |20|

Hahn conclude invece in questo modo: «Il carattere di questa curva elude interamente l’intuizione; in verità dopo poche ripetizioni del processo di segmentazione, la figura che si evolve è cresciuta in modo così intricato che l’intuizione la può a malapena seguire; ed essa ci abbandona completamente... Il fatto è che solo il pensiero o l’analisi logica può seguire questo strano oggetto fino alla sua forma finale» [corsivo mio][7]. Si rivela qui come sia importante l’aver potuto riportare, da parte nostra, la figura ad un calcolo e come assuma rilievo, di fronte ad una simile osservazione il richiamare l’attenzione sulla trasparenza della struttura che si presenta nella formula costruttiva. Questa prospettiva di discorso manca interamente in Hahn benché egli mostri di rendersi conto perfettamente della logica interna della figura nel momento in cui egli traccia il disegno seguente:

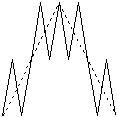
Tuttavia siamo noi a parlare di una logica della figura. Di essa Hahn non ha il benché minimo sospetto, e così, dopo aver prodotto questo disegno tanto istruttivo, passa oltre. L’intuizione, egli dice, operando tra l’altro un pesante spostamento di senso nella parola rispetto agli impieghi che egli stesso ha fatto in precedenza, non riesce a seguire gli intricati percorsi dell’iterazione. Ma sarebbe giusto chiedersi: perché dovrebbe farlo? Si tratta del resto di un problema che, mi sembra, non esiste nemmeno per l’«analisi logica». L’ultima frase secondo cui solo «l’analisi logica può seguire questo strano oggetto sino alla sua forma finale» non può voler dire che la logica riesce a fare ciò in cui l’intuizione fallisce, ma soltanto che, una volta approdati all’infinito attuale, l’oggetto è da parte da parte un «oggetto del pensiero» - un oggetto interamente entrato nell’ideazione matematica. Siamo così tornati a Monsieur de Lapalisse. |21|

Dopo tutto ciò potremo trattare più speditamente del secondo esempio che ci fornisce il destro, non solo per ribadire il nostro orientamento, ma anche di aggiungere alcune considerazioni che ci consentiranno di tirare un poco le fila. |22|

Si tratta di una delle curve «che riempiono lo spazio» proposte da Peano nel 1890. La stessa curva venne discussa da Hilbert nel 1891. |23|

Come nei casi precedenti, la curva è realizzabile attraverso un algoritmo ricorsivo dello stesso tipo di quelli precedentemente proposti. |24|

Si tenga conto che nei linguaggi L-systems i segni privi di regola vengono semplicemente trascurati, e può accadere che una regola per un segno possa essere applicata solo in iterazioni successive alla prima. Ad esempio nel seguente schema nella prima applicazione la regola per il segno B non viene applicata. |25|

La sequenza di figure realizzate nelle prime quattro iterazioni è la seguente:

Nel considerare le figure che presentano ciò che accade nel succedersi delle iterazioni operate sulla stringa potremo certamente essere autorizzati a commentare che ciò che vediamo è che la linea tende a riempire interamente lo spazio, vediamo in certo modo la linea diventare una superficie. L’infittirsi del reticolo fa sì che lo spazio bianco tra le linee diventi sempre più piccolo ed alla fine sarà pienamente occupato. Di fronte agli occhi avremo così un quadrato nero. |26|

Forse si dirà: qui viene considerata la linea percepita e concretamente disegnata, la quale ha, in particolare, uno spessore; ma questa non è matematica! Non è geometria! |27|

Infatti non lo è. Il piano empirico concreto deve essere interamente superato e la curva di Peano-Hilbert deve essere considerata come un oggetto geometrico ideale. Vogliamo allora essere più precisi: oltre a vedere, nel senso usuale del termine, che la linea tende a diventare una superficie, comprendiamo con evidenza che essa tende a diventare una superficie in un senso che non ha nulla a che vedere con la sottigliezza o con lo spessore: si tratta invece di una circostanza che può essere colta ed afferrata nello schema costruttivo, graficamente interpretato, che ne mostra l’«essenza logica», purché naturalmente venga effettuato il passaggio all’infinito attuale che assolve qui un ruolo essenziale. |28|

Il punto del problema sta ora in questo: come è possibile citare una simile curva come esempio di figura «contro-intuitiva», di scacco dell’intuizione, quando l’idealizzazione infinitaria operata dal pensiero può contare, per quanto riguarda la comprensione, su un sostegno intuitivo così cospicuo qual è la struttura visibile della figura? La giustificazione di Hahn consiste nel fatto che sarebbe contrario all’intuizione l’idea che un punto in movimento possa descrivere qualcosa di diverso da una «curva» - ovvero che una curva possa «riempire una superficie». Ma se questa è l’opinione dell’intuizione, si tratta certamente di una intuizione che ha già ragionato molto e che ha compiuto molti passi nella direzione dell’oggetto geometrico astratto. Altrimenti essa sarebbe ferma all’idea che non c’è niente di più facile da capire che una linea possa riempire una superficie. Qualora poi sia acquisita la differenza tra il concreto oggetto percettivo e l’oggetto ideato dal pensiero matematico, l’intuizione avrà ben poco a che ridire rispetto ad un oggetto che per principio si sottrae interamente alla sua giurisdizione e che cade invece in quella del pensiero puro. È in rapporto alle legalità interne a questo campo che talora queste curve sono apparse come dei «mostri», nel duplice senso dell’etimo: delle autentiche «meraviglie» e dei casi «contro-natura». Non per un caso qualsiasi o per una resistenza di forze irrazionali. |29|

Al termine dell’articolo di Hahn, rispunta, spiace dirlo, la saccente superficialità dell’empirismo più rozzo. Quel che ci appare mostruoso e inusuale, finirà con il rientrare nella norma purché sia assecondato dall’educazione e dall’abitudine. Si tratta dunque solo di maggiore o minore familiarità - e Hahn arriva a rendere la parola «intuizione» a tal punto vacua da rendere possibile l’affermazione secondo cui «il concetto di ’differenza di potenziale’ è intuitivo per l’elettricista, ma non per la maggior parte degli uomini»[8]. |30|

Da questa frase, che oscilla tra la banalità e la completa insensatezza, si spicca poi il volo all’idea che con un po’ di educazione e un sistema scolastico moderno tutte le meraviglie e i mostri non esisterebbero affatto, le geometrie non euclidee, gli spazi multidimensionali, e tutto il resto sarebbero «intuitive» quanto lo è la geometria euclidea. Ed anche le curve di Koch, di Peano, ecc., sarebbero considerate come curve qualunque. |31|

Invece si tratta di curve strane! E strane rimarranno per sempre. |32|

Annotazione

Il testo a nostro avviso più importante sul tema della «crisi dell’intuizione» (che assume il carattere di una vasta e penetrante discussione sul concetto di intuizione nell’ambito della riflessione filosofica sulla matematica) è quello scritto da K. Th. Volkert, Die Krise der Anschauung, Vandenhoeck & Rupprecht, Göttingen 1986. In questo libro si dedica una ampia sezione all’«età aurea dei mostri» (pp. 99-157). Della conferenza di Hahn si parla nella parte seconda, storico-sistematica, alle pp. 251-260.

§ 11

§ 13