13

- Per concludere: alcune osservazioni sulla «geometria della natura» e sugli oggetti «fratti»
- Il richiamo alla differenze soggettive del punto di vista
- Il nostro scopo è stato quello di mostrare quanto sia movimentato il rapporto tra l’esperienza e le elaborazioni intellettuali

In certo senso, e in modo inatteso, siamo qui indotti a rammentarci dei nostri precedenti discorsi su Euclide, sulla linea che è «lunghezza senza larghezza». Come se in quella frase si fosse toccato un problema che è ancora in grado di tormentarci. |2|

Le nostre considerazioni sembrano comunque aver proposto una sistemazione della questione che potrebbe essere giudicata abbastanza soddisfacente. Da un lato vi è un calcolo infinitamente iterabile in via di principio; questo calcolo trova il suo strumento concreto in un «traccialinee» con il quale si mostra l’andamento della figura ai diversi livelli dell’applicazione ricorsiva delle regole. Lo spazio entro il quale la curva viene delineata si va riempiendo sempre più, ad ogni successiva iterazione, finché ci troviamo di fronte ad un indiscutibile quadrato nero. |3|

Ma naturalmente sappiamo che ciò accade perché qui la linea ha in effetti una larghezza! Distinguiamo allora chiaramente l’oggetto empirico concreto da un lato e l’oggetto ideale dall’altro. E comprendiamo benissimo che dobbiamo considerare quel riempimento visibile come una sorta di simulazione empirica di un riempimento ideale: come è ideale la curva pensata come interamente tracciata, oppure la stringa infinita di cui quella curva non è altro che una decodificazione grafica. |4|

Eppure proprio nel momento in cui è tempo di chiudere questo nostro saggio sentiamo l’esigenza, non solo di ribadire questo chiarimento, ma di evitare anche che esso, a sua volta, venga inteso in modo troppo rigido. Ciò a cui siamo realmente interessati, da un punto di vista generale, è che sia mantenuta la consapevolezza di quanto sia movimentato il rapporto tra l’esperienza e le elaborazioni intellettuali. |5|

Questo rapporto può essere considerato da più di una angolatura, e se possiamo ritenerci appagati da un modo di impostarlo e di renderci ragione di esso, variando l’angolatura, potrebbero proporsi nuovi problemi capaci di rimettere in gioco il precedente modo di approccio ad esso. |6|

Intanto vi è una circostanza sulla quale occorre richiamare l’attenzione con particolare vivacità: nel momento in cui il pensiero geometrico sta per ricevere una svolta ed un nuovo impulso, quella netta distinzione tra l’oggetto di pensiero da un lato e l’oggetto dell’esperienza dall’altro, viene non tanto messa in questione, quanto temporaneamente sospesa, e ciò accade quasi come un vero e proprio esercizio intellettuale tendente a sondare la possibilità di scoprire, sul piano esperienziale, stimoli ed agganci per nuovi percorsi, nuove inclinazioni possibili dai quali uno stesso problema può essere riconsiderato. |7|

Poiché nei nostri ultimi sviluppi era presente, sia pure assai obliquamente, la «geometria frattale» ed abbiamo ritenuto in precedenza di poter citare come significativa una frase di Mandelbrot, possiamo forse avviarci a tirare le fila ricollegandoci a quello che potrebbe essere immaginato come inizio ideale della sua impresa. |8|

Questo inizio ci sorprende per la sua ovvietà, e ta tanto più ci sorprende il fatto che questa ovvietà sia rimasta per secoli in certo modo fuori campo, quasi a documentare la forza dei paradigmi entro i quali la conoscenza - per una necessità interna di delimitazione tematica e metodica - restringe e determina l’ambito delle cose da ritenersi «rilevanti», emarginando aspetti del reale che si sottraggono ad essi. |9|

Guardiamoci intorno: dove nella natura nella natura troviamo qualcosa come un cilindro un cono o un cubo? Ovvero: quadrati, rettangoli, triangoli, cerchi... queste forme di cui è stata realizzata nei secoli una grande scienza. Possiamo dirci veramente convinti che un albero assomigli ad una piramide? |10|

Dove sono i rami o qualcosa di simile ad un ramo? E che cosa resterebbe della forma vagamente piramidale di un pino o di un abete togliendo di mezzo la struttura della ramificazione? |11|

Improvvisamente apriamo gli occhi, come li apre la folla di fronte alla nudità del re nella fiaba di Andersen. |12|

Mandelbrot fa qui la parte del fanciullo di quella fiaba e nello stesso tempo ci riconduce ancora una volta sul terreno delle forme concretamente esperite orientando il nostro sguardo in una direzione nuova. In certo senso ci si appella inizialmente ad una descrizione più fedele di ciò che ci sta intorno, ma avendo già di mira, naturalmente, il problema di un’estensione della capacità di dominio teorico. Mandelbrot ammonisce a non dimenticare che nello stesso nome della geometria è presente il richiamo alla terra: si tratta di un richiamo che ha numerose implicazioni, ma che intanto attira l’attenzione sul «paesaggio» terrestre, in cui ci sono alberi e foreste, corsi dei fiumi, isole e continenti, montagne, nuvole e pianure. La domanda è allora: in che modo vi può essere una geometria di forme come queste, del crinale di una montagna, delle coste di un’isola, della forma di un albero o di un cespuglio? La risposta a questa domanda non può essere cercata in direzione delle forme euclidee. |13|

Stando unicamente alla nostra esposizione non risulta certo subito chiaro in che senso possa essere interessante proporre il problema delle forme naturali a partire dalle figure ottenute per iterazione ricorsiva. Ciò dipende soprattutto dagli esempi che abbiamo scelto. Essi proponevano per lo più strutture con una forte regolarità interna, per quanto complessa e articolata, talvolta con una certa propensione per la «vetrata» o la «pavimentazione». Abbiamo già avvertito in precedenza che questo risultato dipende dalle peculiarità dei calcoli e non è difficile immaginare, anche a partire dagli esempi precedenti, delle variazioni degli schemi che sono in grado di generare strutture figurali di tipo interamente diverso. |14|

Tra questa enorme varietà di possibilità, vi è anche quella che vengano generate figure che presentano caratteristiche che in qualche modo fanno pensare a forme che troviamo nella natura, e si potrà trattare di forme relativamente regolari, come la forma di un albero, le venatura di una foglia, la forma di una conchiglia; oppure di forme che verrebbero caratterizzate come irregolari, come l’estuario di un fiume, la costa di un’isola o di un continente o il crinale di una montagna. |15|

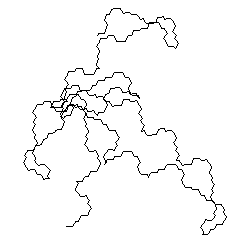
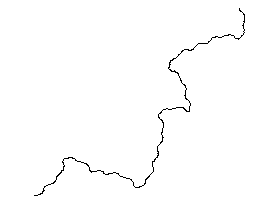
La prima figura che segue è stata ottenuta da questo schema; la seconda dallo stesso schema con angolo a 32°, entrambe alla quarta iterazione.

Solo con un’attenta osservazione si riscontreranno qui delle ricorrenze, e l’apparenza di casualità potrà essere accentuata nel proseguimento delle iterazioni. Si riveda a questo proposito la curva di Koch e le sue successive iterazioni: ad ogni iterazione la curva diventa sempre più frastagliata, sempre più fratta. Nella stessa scelta di questo termine - oggetto frattale, geometria frattale - piuttosto che sull’iterazione l’accento viene fatto cadere sulla «spezzatura». I «mostri» non cominciano con le curve strane e straordinarie di Weierstrass, di Koch, di Peano o di Hilbert: in realtà è un «mostro» in potenza già la più semplice delle «spezzate». Nello stesso tempo avviene una modificazione prospettica assai singolare: i mostri sono tanto poco tali da essere indicati come possibili modelli di forme naturali. |16|

Ripensiamo all’esempio famoso proposto da Mandelbrot della misurazione della costa della Gran Bretagna. Sono almeno due gli aspetti che meritano qui di essere messi in rilievo: anzitutto si ritorna a riflettere su un problema di misurazione, e precisamente su un problema, almeno in prima apparenza, del tutto empirico. In secondo luogo si avanza in certo senso la pretesa di ritrovare su questa terra quell’infinito attuale che appartiene invece al paradiso delle ideazioni matematiche. |17|

Si verifica infatti per una costa qualcosa di simile a ciò che si verifica per la curva di Koch. Pensiamo ad un golfo visto dall’alto e molto di lontano. Esso ci apparirà con quell’andamento caratteristicamente semicircolare che ci fa appunto parlare di esso come di un golfo. Ma non appena il nostro sguardo si avvicina ad esso, la linea semicircolare ci apparirà sempre più frastagliata. Di fronte a noi vi sarà eventualmente solo una porzione del golfo intero, ma questa porzione sarà a sua volta fatta di golfi più piccoli ciascuno dei quali, ad un sguardo più ravvicinato, apparirà fatto di golfi, ecc. |18|

Ora ci chiediamo: fino a che punto procederemo in questo mutamento di scala? Non potremmo continuare fino ad insenature i cui estremi distano di pochi metri, e ancora oltre, di pochi centimetri, e ancora oltre? Che ne sarebbe allora della lunghezza della costa e della sua possibile misurazione? Nel proporre questo esempio Mandelbrot osserva che la lunghezza della costa è «praticamente infinita». In realtà, se se si pone il problema della misurazione di una costa, ciò avverrà per determinati scopi e sono questi scopi a determinare il punto di tollerabilità della rettificazione, il punto cioè nel quale termina l’interesse di ogni ulteriore variazione di scala. Il problema della lunghezza infinita sorge solo se si ha nella testa la curva di Koch - o qualche altra dello stesso tipo. La costa della Gran Bretagna diventa allora un puro pretesto in rapporto alla discussione di una questione tutta teorica. |19|

Nello stesso tempo è anche vero che si potrebbe sostenere che una curva frattale di un certo tipo può essere considerata un modello per una costa in genere: qualcosa di capriccioso come una costa, che noi possiamo al più descrivere o rappresentare nel senso di una immagine-copia può, a quanto sembra, essere invece artificialmente costruito, può essere simulato come se fosse prodotto, anziché da sommovimenti tellurici, dal gioco del mare contro le rocce, da un algoritmo iterativo. O più precisamente: la forma di una costa è determinata da diversi fattori di ordine fisico, da una catena più o meno complessa di eventi causali: la sua forma può essere descritta nel modo in cui essa si presenta e indagata nella rete degli eventi causali che la hanno generata. Ma di fatto disponiamo di un calcolo che è in grado di costruire una configurazione tipologicamente analoga e non ce la sentiamo di sostenere che ciò non significhi proprio nulla, che questa circostanza sia del tutto disomogenea alle precedenti e che di essa non possiamo farcene proprio nulla. |20|

Al contrario si può sostenere che proprio questa simulazione, questa artificializzazione, questa ricerca di modelli fa parte degli scopi essenziali del conoscere. Ed alle obiezioni secondo le quali avremmo, da un lato, a che fare con strutture rigorosamente deterministiche e dall’altro con processi in cui la «casualità» assolve comunque una funzione significativa si può rispondere segnalando la possibilità di prendere ulteriori provvedimenti, ad esempio quello di rendere più duttili i calcoli oppure di realizzare delle attenuazione o degli indebolimenti di concetti di base. |21|

Il calcolo, una volta istituito fa esattamente quello che deve fare; ma siamo noi a istituire i calcoli. Nella struttura dei calcoli possono essere previste regole particolarmente complesse e modi complessi di impiegare le regole, oppure addirittura modificazioni casuali delle condizioni[1]; all’autosimilarità in senso stretto e rigoroso, come è esemplificata dalla curva di Koch, è possibile sostituire una nozione più elastica di quasi-autosimilarità, di autosimilarità statistica. |22|

Vi è un singolare cammino che conduce dalla ripetizione - che è certamente una delle sorgenti di strutture ordinate - all’elemento caotico, dalla regola all’assenza più o meno apparente di regole. Si comprende anche che la questione qui sfiorata tende a superare una problematica puramente morfologica. La terra di cui si parla è anche la terra in quanto sede di fenomeni naturali di ogni genere, di fenomeni metereologici, di trasformazioni biologiche, fisiche e chimiche, ed è naturalmente la terra in quanto pianeta che partecipa ad una vicenda cosmica. Fin dall’inizio la geometria «frattale» avanza la pretesa di essere una «geometria della natura» - una dizione che prospetta un pensiero geometrico già tutto rivolto, fin dai suoi primi passi, al problema di possibili applicazioni. |23|

In realtà si potrebbe forse sostenere che questo riferimento alle applicazioni si presenti anche troppo a ridosso dell’elaborazione teorica, e che questa sia di conseguenza dominata, più che dalla preoccupazione della perfezione formale dei concetti, dalla loro utilizzabilità. |24|

Dobbiamo ammettere che anche dal nostro punto di vista, che si limita scientemente alla problematica morfologica, questo accento posto sulle forme naturali suscita qualche perplessità, nonostante l’interesse intrinseco dell’argomento. Tuttavia va preso atto del fatto che una sorta di speciale ritorno all’empirico, al naturale, al reale, o comunque più ampiamente ad una tematica non solo geometrica, ma fisica in un senso ampio del termine, è stato uno dei motori della nuova geometria «frattale». Questo richiamo assume a tratti anche l’andamento di una riflessione sulla stessa struttura della percezione e sulle modalità dinamiche delle costituzioni percettive dell’oggetto. |25|

Si presti nuovamente attenzione al modo in cui è stato posto il problema della costa e quindi anche al modo in cui è stato riproposta l’idea della lunghezza infinita. La concretizzazione di questa massima astrazione ripropone le differenze soggettive del punto di vista - più da vicino, più di lontano - che fanno parte dell’esperienza della realtà, ed è appena il caso di rilevare come questa circostanza sia significativa nel contesto dei problemi intorno ai quali si sono sviluppate prevalentemente le nostre discussioni. Il concetto puro non esita ad imbastardirsi riprendendo il contatto con l’esperienza, ricevendo di qui nuovi stimoli e nuove direzioni di sviluppo. |26|

Indicativo dello stesso problema è il modo in cui viene introdotta la nozione di dimensione frattale[2]. La considerazione che sta alla base di questa nozione è puramente matematica: è interessante tuttavia notare che nel momento in cui essa viene qui fatta valere ci si richiama alle relatività fenomenologiche della cosa materiale, agli «adombramenti prospettici» di cui parlano i fenomenologi. |27|

La dimensione è forse qualcosa che appartiene all’oggetto come tale come un suo attributo specifico e caratterizzante? Consideriamo allora un gomitolo di lana Quale dimensione dobbiamo attribuirgli? Dovremmo dire che esso è un oggetto sferico tridimensionale? In effetti esso ci apparirà così solo se lo guardiamo ad una certa distanza. Invece, guardato a breve distanza e con una lente di ingrandimento non vedrò affatto il gomitolo di lana, ma vedrò il filo, ed eventualmente vedrò i fili di cui è composto il filo di lana: fili sottilissimi che mi sembreranno senza spessore. Perché mai di un filo così sottile dovrei dire che esso ha tre dimensioni? Eppure con una lente abbastanza potente questi fili sottilissimi mi potranno apparire come colonne. A cominciare da questa relativizzazione della nozione di dimensione e facendo notare la varietà delle situazioni che si possono presentare già a livello percettivo, l’idea di una possibile dimensione intermedia, ad esempio tra l’1 e il 2, può ricongiungersi con un’elaborazione matematica già predisposta e che può avere un’origine e una giustificazione interamente diversa. |28|

Il purismo matematico potrà anche alzare le spalle di fronte ad una mossa che sembra dovuta puramente agli interessi della divulgazione. Da parte nostra, diremo invece che gli interessi della divulgazione siano i benvenuti se suggeriscono una riflessione di ampio respiro che riguarda le tensioni tra concetti ed intuizioni, tra formazioni del pensiero puro e formazioni esperienziali. Queste tensioni talora si attenuano e si stabilizzano, talora ridiventano effervescenti, e lo ridiventano in particolare nei grandi momenti innovativi, quando si intravvedono vie nuove e nuove possibilità di elaborazione teorica. Allora invece di chiare distinzioni potremo avere la sensazione di precipitare nell’ambiguità: da un lato, l’esempio del gomitolo di lana è rozzamente empirico, dall’altro esso si situa in una direzione che promuove nuove vie del pensiero e nuovi modi di approccio teorico. Certamente possiamo sempre adagiarci in contrapposizioni elementari - in esse conviene persino cercare un sostegno quando è necessario riordinare le idee: ma con l’attenzione in ogni caso sempre rivolta ad apprezzare gli impulsi che provengono dal concreto dell’esperienza e la grandezza e l’audacia della speculazione logico-concettuale. |29|

§ 12

Fine del volume