IV

Filosofia della matematica

1.

Vogliamo ora dedicare un po’ di attenzione alla filosofia della matematica del Tractatus. Essa gravita interamente intorno a due nozioni: quella di equazione e quella di numero Delle due, la più generale è la prima. La matematica consta di equazioni (6.2(b)), e l’equazione sta alla matematica come la tautologia alla logica. Ad essa noi dobbiamo fare riferimento per una sua caratterizzazione di principio.

Equazioni sono espressioni che hanno forma «a=b» (oppure «a=a»). Potremmo intendere un’espressione di questo genere nel senso suggerito dalla loro formulazione verbale: «a è eguale a b». I segni «a» e «b» saranno allora nomi, e quell’espressione ci appare come una proposizione che afferma qualcosa intorno a certi oggetti, e precisamente il sussistere tra essi di una certa relazione designata dal segno «=». Un richiamo al principio leibniziano degli indiscernibili potrà servire ad illustrare ciò che si intende con la posizione di questa relazione; ed il suo sussistere giustificherà, nel simbolismo, una regola di sostituibilità reciproca dei segni che stanno alla sinistra ed alla destra del segno di eguaglianza.

La linea dell’impostazione di Wittgenstein deriva da una inversione di questo punto di vista: intendiamo l’espressione «a=b» anzitutto come una regola di sostituzione tra i segni. Nella posizione di una simile regola non abbiamo ovviamente bisogno di richiamarci al significato dei segni. Se poi ad «a» o, alternativamente, a «b», viene attribuito un significato, la regola pone «a» e «b» come segni che hanno lo stesso significato. Diremo così che due segni hanno lo stesso significato se per essi vale una regola di sostituzione. In questo modo restiamo all’interno di un discorso che riguarda soltanto il simbolismo, e non ciò di cui esso tratta. In particolare non abbiamo bisogno di assumere che non possano darsi due cose che abbiano in comune tutte le loro proprietà (5.5302); e neppure di considerare l’eguaglianza come una relazione tra cose (5.5301), come induce a ritenere la formulazione proposizionale di un’equazione.

Vediamo così anche in che senso andrà intesa la differenza d’uso del segno «=» quando esso si presenta tra segni percettivamente diversi oppure tra segni percettivamente eguali. È chiaro che del segno «=» viene fatto un uso proprio solo se alla sua sinistra ed alla sua destra vi sono segni di forma percettivamente diversa, la regola «a=a» non avendo bisogno di essere formulata. D’altro lato, una regola di forma «a=b» non può introdurre alcun simbolo nuovo, ma soltanto nuovi segni per gli stessi simboli. Se introduciamo in questo modo nuovi segni, ciò può accadere soltanto come un «espediente della rappresentazione» (4.242). Siamo qui di fronte ad una semplice ripresa di un aspetto della tematica della teoria del simbolismo. Poiché in ogni caso tutto ciò che un linguaggio può dire, lo può dire soltanto con i suoi segni primitivi, possiamo affermare che «il segno di eguaglianza non è una parte costitutiva essenziale dell’ideografia» (5.533), che in un linguaggio in cui allo stesso oggetto corrisponda lo stesso segno, ad oggetti diversi segni diversi (5.53), del segno dell’eguaglianza non vi sarebbe bisogno[1].

«Se indichiamo lo stesso oggetto una volta con «a», l’altra con «b» nel linguaggio vi sono allora più segni di quanti siano necessari per la raffigurazione dei fatti. Noi dobbiamo ora spiegare che questa eccedenza dei segni non significa nulla, che la differenza dei segni non è un momento raffigurativo del simbolismo. Ciò accade mediante la regola segnica «a=b». Se conosco il significato del segno a allora questa regola mi dice che cosa debbo intendere con «b». Questa regola non parla della realtà. Essa non dice: gli oggetti indicati da «a» e da «b»si trovano l’uno con l’altro in un rapporto di identità; ma essa tratta dei segni stessi. Essa è una determinazione relativa all’uso dei segni. La falsa concezione dell’identità sorge non appena si assumono i segni con il loro significato. Allora si crea l’apparenza che «a=b» sia una proposizione che per mezzo dei segni - attraverso i segni - parli della realtà. Ma che l’identità sia soltanto una regola dei segni lo vediamo dal fatto che essa scompare non appena ci serviamo di un linguaggio che presenta ogni oggetto mediante un unico segno» [2] Anche in rapporto alle equazioni, possiamo dire che esse non esprimono alcun pensiero (6.2 e 6.21). In esse non si parla della realtà, né in genere di qualcosa: come le tautologie, esse rinviano a regole del linguaggio.

2.

Prima di accingerci ad illustrare la nozione di numero, dobbiamo compiere una digressione che ci riporti alla tematica della proposizione, e precisamente al problema che si presenta nel Tractatus sotto il titolo di «forma generale della proposizione».

a) Indichiamo i termini di questo problema. Una proposizione è un complesso di segni capaci di esprimere un senso. In che modo i segni debbano essere associati, in un determinato linguaggio, per dare luogo ad una proposizione, ciò dipende dai modi di costruzione grammaticale peculiari a quel linguaggio. Ma poiché ogni proposizione è un complesso di segni capace di esprimere un senso, le proposizioni di ogni linguaggio debbono avere qualcosa in comune; questo è appunto ciò che la proposizione è nella sua «essenza»: la forma generale della proposizione (5.47 e 5.471).

Dovremo dunque prescindere dalle forme particolari che le proposizioni possono assumere nei diversi linguaggi, dal momento che la questione della forma generale della proposizione è certamente ancora una questione grammaticale, ma propriamente una questione di «grammatica logica» (in un’accezione diversa da quella in cui abbiamo usato in precedenza questa espressione). Il compito di dare una descrizione della forma generale della proposizione - osserva Wittgenstein in modo abbastanza aggrovigliato - consiste nel «dare una descrizione delle proposizioni in un simbolismo qualunque», di dare cioè una descrizione che sia tale che un senso possa essere espresso da un simbolo che sia conforme a quella descrizione; oppure che, dato un simbolo che sia conforme a quella descrizione, esso possa esprimere un senso (4.5).

Che vi sia una forma generale della proposizione significa: non può accadere che, ad un certo punto, si presenti una proposizione la cui forma non sia possibile prevedere. Altrimenti noi sapremmo dall’esperienza che qualcosa è una proposizione - dovrebbe «venire un momento in cui, improvvisamente, facciamo una nuova esperienza, per così dire un’esperienza logica. Questo naturalmente è impossibile» (Q, p. 176).

E poiché possiamo prevedere solo ciò che noi stessi costruiamo (5.556), il nostro problema diventa allora quello di determinare il modo di una costruzione, quindi 1’ operazione da cui ogni proposizione viene generata e il metodo di questa generazione.

b) In un’operazione, in generale, distinguiamo la base a cui essa è applicata da ciò che otteniamo applicando l’operazione ad una base: il suo risultato.

Base di un’operazione potrà essere il risultato di un’operazione. Oppure: un’operazione può essere applicata al risultato di un’operazione. E come caso particolare: al «proprio» risultato. Secondo la terminologia di Wittgenstein, parliamo di applicazione successiva dell’operazione (5.251).

Con serie formale intenderemo una serie di risultati operazionali ottenuti nell’applicazione successiva di un’operazione ad una base.

La nozione di serie formale, peraltro, viene introdotta da Wittgenstein in modo indipendente da quella di operazione come una serie che sia ordinata da una relazione strutturale (4.1252). In tal caso consideriamo la serie, per così dire, staticamente. Ora dobbiamo precisare: la presenza di una relazione strutturale tra gli elementi della serie rinvia ad un nesso generativo, ad un principio di generazione e di costruzione. L’operazione si esprime, e in certo modo si risolve, in una relazione tra la struttura della sua base e la struttura del suo risultato (5.22).

Vogliamo ora indicare mediante un segno la forma di un elemento qualsiasi della serie - il suo termine generale (5.2522).

Se con la lettera «O» indichiamo una certa operazione, il termine generale della serie generata per applicazione successiva ditale operazione ad una certa base «a» potrà essere presentato dal segno: (a, x, Ox), dove x è una variabile per un elemento qualsiasi della serie. Questo segno presenta la forma di un elemento qualsiasi della serie nella stessa misura in cui presenta lo schema operativo [3] da cui essa è generata.

c) Rammentiamo la distinzione che abbiamo introdotto a suo tempo tra concetti effettivi e concetti formali. Il concetto di proposizione lo dobbiamo porre senz’altro tra i concetti formali. Introducendo quella distinzione Wittgenstein sottolineava inoltre che i concetti formali non possono essere presentati da una funzione, ma da una variabile. Quelle osservazioni ricevono il loro effettivo significato solo a questo punto. Un concetto formale, a differenza dei concetti effettivi, rinvia ad un’operazione, esso è cioè la forma comune degli elementi di una serie di risultati operazionali. Questa forma è presentata dal segno del termine generale della serie - segno che è, appunto, una variabile (5.2522).

In rapporto al concetto di proposizione si tratterà allora di indicare l’operazione che genera, a partire dalle proposizioni elementari assunte come basi, la serie delle proposizioni. O in altro modo: di esibire lo schema operativo di questa serie, schema che descrive i simboli mostrandone la struttura e che in questo modo dice che cosa è una proposizione.

È qui senz’altro opportuno attenerci alle semplici convenzioni notazionali proposte da Wittgenstein.

Sia «» una variabile di proposizioni e «» il campo di tale variabile, che sarà di volta in volta determinato (5.501). Con «N()»indichiamo un’operazione che applicata a proposizioni genera una proposizione che è vera solo se sono false tutte le proposizioni che appartengono a «» (5.502).

Chiamiamo negazione tale operazione. Come è noto Wittgenstein utilizza qui il risultato dovuto a Sheffer secondo cui è sufficiente, nel linguaggio della logica degli enunciati, servirsi di un unico connettivo primitivo caratterizzato in questo stesso modo come funzione di verità e sul piano notazionale dal segno «¯» frapposto ai segni proposizionali[4]. Poiché la negazione viene definita qui nei termini dell’operatore «¯» (ponendo alla sua sinistra ed alla sua destra lo stesso segno proposizionale) sembra improprio parlare di negazione in rapporto ad esso. Ma non si fa altro che creare confusione parlando in rapporto all’operatore di Sheffer di negazione «congiunta» o «simultanea». Va invece soltanto messa in rilievo la differenza notazionale L’operatore in questione viene introdotto da Wittgenstein per un numero qualsiasi di basi, e in particolare per un’unica base. Bisogna perciò prestare attenzione al modo in cui deve essere inteso il segno in N(). Noi disponiamo, per dirla in breve, di una lista di proposizioni. Il campo dei valori di , viene di volta in volta isolato su questa lista, ed esso è la totalità dei valori di (come casi particolari abbiamo appunto l’isolamento di un’unica proposizione e l’«isolamento» dell’intera lista).

Si vede subito allora che l’operatore «N()»può essere caratterizzato come negazione nella misura in cui la negazione nel senso usuale non è che un suo caso particolare[5].

Precisato questo punto, la forma generale della proposizione sarà indicata dalla formula: (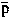, N()) in cui 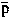sarà una lista di proposizioni elementari. Diciamo così che ogni proposizione, se non è elementare, è ottenuta per applicazione successiva della negazione ad una lista di proposizioni elementari[6].

Il metodo di Wittgenstein per il calcolo delle condizioni di verità suggerisce la seguente rappresentazione della derivazione operativa di proposizioni in rapporto ad un sistema di due proposizioni elementari:

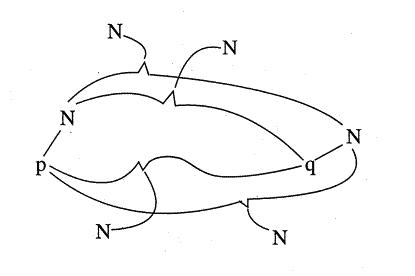
Abbiamo qui riuniti gli schemi:

Si potranno poi formare iterativamente ulteriori schemi. Ad esempio:

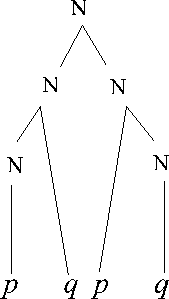
E così via [7].

d) Un cenno conclusivo all’interpretazione dei quantificatori. In realtà il tratto sovrapposto a in era già un segno di universalizzazione. L’universalizzazione riguarda perciò la base, non l’operazione - ed in generale noi dobbiamo affermare che i segni di quantificazione sono di specie diversa dal segno della «negazione» ed in genere dai segni delle «funzioni di verità». «Io separo tutti dalla funzione di verità» (5.521). Abbiamo detto che è una variabile di proposizioni. Basterà allora assumere che il campo dei suoi valori sia la totalità dei valori di una funzione proposizionale per ottenere l’interpretazione di un’espressione di forma «N()» nei termini di una proposizione quantificata che contiene quella funzione proposizionale (5.52).

Ciò avviene naturalmente al prezzo che si postuli la specificabilità della lista di tutte le proposizioni che sono valori di una certa funzione.

Questo è peraltro una conseguenza necessaria dell’empirismo del Tractatus. Il criterio che vincola la sensatezza alla verificabilità non può conoscere a questo punto un’eccezione. Perciò «tutte le cose» deve essere qualcosa di simile ad una «descrizione in luogo di "a e b e c"» (Q, p. 104) [8]. Del resto fin dall’inizio si vincolava la possibilità raffigurativa della proposizione alla completezza ed alla determinatezza della descrizione da essa effettuata. La presenza di una funzione proposizionale all’interno di una proposizione quantificata mostra che in essa non tutto è ancora determinato e questa determinazione è possibile solo se è possibile la specificazione degli elementi del complesso a cui essa rinvia (3.24(c)).

Questa interpretazione delle proposizioni «generalizzate» consente inoltre una precisa chiarificazione della differenza tra proposizioni «logiche» e proposizioni «universali». Anche una descrizione «generalizzata» del mondo, una descrizione cioè nella quale non compaiono proposizioni elementari ma solo proposizioni che contengono funzioni proposizionali, resta vincolata al terreno empirico nella misura in cui debbono poter essere specificate le proposizioni elementari che sono valori di quelle funzioni (5.526).

Wittgenstein certamente non sostiene che una simile descrizione sia esattamente la stessa cosa che una descrizione effettuata mediante proposizioni elementari. Per l’individuazione del mondo così descritto debbono essere effettuate le coordinazioni necessarie. Ma il punto che Wittgenstein intende sottolineare è che anche in questo caso non viene meno un riferimento contenutistico, un riferimento a contenuti indeterminati che tuttavia debbono poter essere determinati.

Quando diciamo che una proposizione non dice nulla, vogliamo sottolineare anche che la sua generalità va intesa in tutt’altro senso, che essa è una generalità «essenziale» o «formale» di fronte alla generalità «empirica» o «accidentale» (6.031) (Q, p. 104).

Inoltre è chiaro che mettere in questione questa interpretazione dei quantificatori, non avrebbe il carattere di una critica di dettaglio, ma piuttosto quello di aprire una breccia nell’empirismo del Tractatus e nell’intelaiatura teoretica nella quale esso è intessuto. Di fronte a questo problema noi procediamo, al contrario, riconducendo i vari fili di questo empirismo a quest’unico nodo: «La forma generale della proposizione è: le cose stanno così» (4.5(c)), perchè una proposizione deve, in generale, poter esprimere un senso, cioè presentare uno stato di cose possibile. E la negazione appartiene costitutivamente al concetto di proposizione nella stessa misura in cui la possibilità di essere vera o falsa rappresenta il carattere della sua sensatezza.

D’altro lato, nella formula della forma generale della proposizione troviamo probabilmente anche l’espressione più forte dell’empirismo logico del Tractatus. Attraverso di essa noi ripetiamo ancora una volta che il «contenuto» della proposizione è dato dalle proposizioni elementari dal momento che «l’operazione non enuncia nulla, ad enunciare è solo il suo risultato, e questo dipende dalle basi dell’operazione» (5.25(b)). Dire che ogni proposizione è il risultato dell’applicazione successiva della negazione a proposizioni elementari significa, in certo modo, fondare la tesi di estensionalità nella stessa forma logico-grammaticale della proposizione.

Resta il fatto che il problema della forma generale non può essere proposto in rapporto alle proposizioni elementari. Non vi è una forma comune a tutte le proposizioni elementari. Ammettere questo sarebbe ammettere il loro possibile ordinamento in una serie, quindi la sussistenza tra esse di relazioni interne. Ma, come sappiamo, gli stati di cose sono indipendenti - e così anche le proposizioni che li descrivono. Certo, noi diciamo che la proposizione elementare ha una forma logica, e precisamente che essa ha la stessa forma dello stato di cose che essa presenta. Ma la forma dello stato di cose e la forma della proposizione sono l’una nell’altra come il sigillo nel guanto di cera. Perciò la forma logica della proposizione elementare è sempre particolare. Certo, noi abbiamo un «concetto» della proposizione elementare (5.555), noi sappiamo che essa è una concatenazione di nomi - ma in nessun modo ciò rappresenta qualcosa come una forma comune, nel senso in cui ne abbiamo parlato fin qui. La proposizione elementare non è qualcosa che noi costruiamo - e per questo non possiamo «rispondere a priori alla questione di tutte le forme possibili di proposizioni elementari» (5.55).

Le proposizioni elementari sono date. Tutto il resto è algoritmo.

3.

Il modo dell’approccio di Wittgenstein al problema del numero è ormai interamente a portata di mano: come il concetto di proposizione, anche il concetto di numero è un concetto formale e la sua interpretazione deve essere effettuata rinviando alla nozione di operazione. Notiamo tuttavia subito un’importante differenza. Noi abbiamo illustrato la nozione di operazione in generale attraverso i suoi momenti costitutivi essenziali - la base, il risultato, l’iterabilità; ed abbiamo poi parlato di una particolare operazione, la negazione, come operazione che genera la serie delle proposizioni quando sia successivamente applicata alle proposizioni elementari assunte come basi.

Il modo della connessione del numero con l’operazione è interamente diverso: qui non abbiamo bisogno di prendere in considerazione nessuna operazione particolare. Il numero è una nozione fondata direttamente in quella di operazione in generale.

Tutto il problema consiste - nella presentazione di Wittgenstein - nell’istituire la sostituibilità di ogni elemento generato dallo schema:« (x, x, W(x))» in cui «x» e «W» saranno rispettivamente variabili di basi e di operazioni e «x» un elemento qualsiasi della serie, con ogni elemento generato dallo schema: «(W⁰x, Wⁿx, Wⁿ⁺¹ x)». A ciò provvedono le seguenti definizioni:

I. x = _def W⁰x

II. WWⁿx = _defWⁿ⁺¹

Mentre le definizioni:

0+1 = _def 1

0+1+1=_def 2

0+1+1+1= _def 3

.................................

forniscono abbreviazioni per i segni in esponente.

Questo è tutto quanto viene presentato nella proposizione 6.02: viene cioè introdotto un simbolismo [9]; e da esso dobbiamo desumere la concezione del numero del Tractatus. In base alle considerazioni precedenti, possiamo illustrare la prima definizione dicendo che il segno «O» posto in esponente ad un segno operazionale indica che nessuna operazione è stata applicata alla base; mentre la seconda definizione può essere illustrata dicendo che un segno «+1» indica l’applicazione successiva dell’operazione. In breve, attraverso questo simbolismo, Wittgenstein spiega che la nozione di numero deve essere interpretata riferendola all’iterabilità dell’operazione. Volendo formulare la cosa tenendo conto delle particolarità del simbolo introdotto diremo che il numero è «l’esponente di operazioni» (6.021) [10].

Rammentiamo ora la possibilità di considerare una serie formale staticamente, prescindendo cioè dal riferimento all’operazione generatrice e considerando unicamente la relazione strutturale che sussiste tra i suoi elementi. È chiaro allora che in rapporto al problema del numero, non viene in questione nessuna delle varie relazioni strutturali dipendenti dalla particolarità dell’operazione - ma solo la relazione di successione - quella relazione, cioè, che «esprime» unicamente l’iterazione dell’operazione. Tale relazione dunque non va intesa come una relazione particolare tra le altre relazioni particolari per la stessa ragione per cui non distinguiamo, tra le operazioni, quelle iterabili e non iterabili (e perciò nemmeno la serie formale dei numeri dovrà essere intesa come una serie formale tra le altre)[11].

4.

La matematica, dicevamo all’inizio, consta di equazioni. Ma qual è il significato effettivo di questa affermazione? In fondo lo possiamo cogliere proprio dalla presentazione della nozione di numero. Qui non si è fatto altro che introdurre un simbolismo - quella concezione veniva formulata attribuendo ad esso un’interpretazione. La nostra conclusione era: il segno numerico non è un nome, non si riferisce ad oggetti. Esso «significa» l’iterazione dell’operazione.

Ma in nessun modo abbiamo bisogno di mantenere una presa sul significato. Nella matematica «noi procediamo da un certo numero di equazioni sostituendo espressioni con altre corrispondentemente alle equazioni» (6.24).

La questione dell’aritmetica, della sua costruzione, è una questione di sintassi logica, nella quale «il significato di un segno non deve mai assolvere una funzione; la sintassi logica deve stabilirsi senza parlare del significato di un segno; essa può presuppone solo la descrizione delle espressioni» (3.33).

Le definizioni iniziali indicano soltanto delle possibilità di sostituzioni segniche; istituiscono regole di trasformazione dei segni - in breve, istituiscono un calcolo. E gli ulteriori sviluppi di questo calcolo sono interamente affidati a definizioni ulteriori, attraverso le quali vengono stabilite nuove possibilità di trasformazione, si introducono nuovi segni, e così via. Dire che la matematica consta di equazioni non significa che questo: essa consta interamente di calcoli. «Nella matematica tutto è algoritmo, nulla significato» [12]. Ad esempio, introduciamo la definizione:

W^n´m x =_def (Wⁿ)^m

che mostra in che modo nel nostro calcolo possa essere introdotto il nuovo segno «´» e in che modo dobbiamo calcolare con esso. Wittgenstein presenta anche un’esemplificazione di un simile calcolo (6.141) che vogliamo presentare per intero con la sola modificazione consistente nell’aggiunta di un esponente «1» ai segni operazionali privi di esponente:

=W¹W¹W¹W¹x=W^{1+ 1+ 1+ 1} x=W⁴x

Ciò che qui vi è di caratteristico nell’uso dei segni «´» e «+» è che il calcolo con essi avviene attraverso la loro progressiva eliminazione dal simbolismo sino alla riduzione dell’espressione numerica in una espressione che ha forma di una successione di cifre «1».

Vi è anche un altro accenno che merita particolare attenzione. «È una proprietà del segno ‘1+1+1+1’ la possibilità di concepirlo quale »(1+1)+(1+1)« »(6.231). Diciamo cioè che la validità dell’equazione «2+2=4» deve essere colta nel segno stesso - che essa si mostra quando, operando le sostituzioni, si siano posti i segni nella loro forma primitiva. In rapporto alle tautologie si diceva: «Si può concepire la logica in modo tale che ogni proposizione sia la sua propria dimostrazione» (6.1265). Ed analogamente ora diciamo: «L’essenziale del metodo matematico è lavorare con equazioni. Su questo metodo si fonda il fatto che ogni proposizione della matematica debba comprendersi da sé» (6.2341). Oppure: «Se due espressioni sono connesse dal segno di eguaglianza, ciò vuol dire che esse sono sostituibili l’una all’altra. Ma se è così, ciò deve mostrarsi dalle espressioni stesse» (6.23). L’«analiticità» delle espressioni matematiche, la loro validità e indipendenza dall’esperienza deve essere ridotta e giustificata, come nel caso delle proposizioni logiche, all’interno delle regole del linguaggio. Le trasformazioni dei segni che operiamo nel calcolo hanno in entrambi i casi la funzione di portare all’evidenza della percezione - che anche in questo caso distinguiamo ed anzi contrapponiamo alla evidenza psicologica - questa validità che può essere «nascosta» dalla forma o dalla complessità del segno.

Siamo così in presenza di quell’aspetto «intuizionistico» - nel senso peculiare che abbiamo attribuito a questo termine in rapporto al Tractatus - che abbiamo riconosciuto come l’aspetto che motiva e illustra la tematica del «mostrare» in connessione con la teoria dell’immagine e che rappresenta il centro della filosofia della logica e della matematica proposta da Wittgenstein.

Quest’aspetto si presenta qui in un’accentuazione particolarmente forte. Che sia una proprietà del segno «1+1+1+1» il potersi presentare come «(1+1)+(1+1)», lo potremmo dimostrare provando l’equazione «2+2=4», ed illustrare con un ’immagine come questa [13]:

Ciò che importa è il modo in cui è fatto il segno aritmetico; ed è lecito pensare che, secondo Wittgenstein, anche le «leggi fondamentali dell’aritmetica» - e tra queste il principio di induzione completa - debbono essere considerate anzitutto come regole sintattiche che sono giustificate direttamente nella struttura del segno aritmetico.

Si tratta di vaghe allusioni. Tuttavia, prendendo le dovute distanze, è interessante un breve richiamo alla «teoria elementare dei numeri» in David Hilbert. In entrambi i casi abbiamo infatti a che fare con segni numerici intesi come figure concrete, come oggetti della percezione, ed in questo senso con oggetti «intuitivi» in rapporto ai quali operiamo secondo l’evidenza della percezione. In entrambi i casi le «leggi» saranno regole immanenti nella struttura del segno aritmetico e fondate in esso. Ma la differenza comincia già con l’apparire dal primo passo che compie Hilbert, dalla descrizione in parole della struttura del segno numerico.

«Nella teoria elementare dei numeri noi abbiamo un oggetto iniziale e un processo di sviluppo. Entrambi li dobbiamo determinare intuitivamente. Il modo particolare di questa determinazione è qui inessenziale: si deve soltanto mantenere la scelta, una volta fatta, per l’intera teoria. Noi scegliamo come cosa iniziale, la cifra 1 e come processo di sviluppo l’apposizione di 1.

Le cose che, prendendo le mosse dalla cifra 1, otteniamo mediante l’applicazione del processo di sviluppo, ad es.

1, 11, 111

sono figure della seguente specie: esse cominciano con 1 e terminano con 1; ad ogni 1 che non si trovi già al termine della figura segue un 1. Esse vengono ottenute mediante l’applicazione del processo di sviluppo, quindi attraverso una composizione, che giunge concretamente ad una conclusione, e questa composizione può essere perciò anche fatta regredire mediante una scomposizione che proceda di passo in passo» [14].

In luogo di ciò presentiamo soltanto lo schema operativo:

(1, n, n1)

Esso mostra come e fatto un segno numerico mostrando in che modo deve essere costruito.

L’addizione viene spiegata da Hilbert in parole in questo modo: «Se una cifra b coincide con una parte di a, allora la parte restante è una cifra c; si ottiene così una cifra a apponendo la cifra c alla cifra b in modo tale che 1’ 1 con il quale e comincia viene fatto seguire all’1 con il quale b termina nel modo del processo di sviluppo. Questo modo di composizione di cifre lo indichiamo come addizione, e usiamo per essa il segno +».

La moltiplicazione in quest’altro: «La moltiplicazione può essere definita come segue: a.b significa la cifra che si ottiene dalla cifra b sostituendo nella costruzione sempre la cifra i con la cifra a, cosicché si forma anzitutto a effettuando poi l’apposizione di a in luogo di ogni 1 che si presenta nella formazione di b» [15].

Simili illustrazioni non sono intuitive solo perché riguardano oggetti della percezione, ma anche perché sono vaghe (ad esempio, non sappiamo che cosa significhi esattamente «apposizione»).

In luogo di quelle spiegazioni per l’addizione e la moltiplicazione, come abbiamo visto, noi istituiamo regole della sintassi. E vi è una regola, ad esempio, che istituisce la eliminabilità della figura «+», una regola che istituisce la sostituzione della figura 2 con la figura 11, ecc.

Queste regole compaiono in equazioni, e non in enunciati provvisti di senso.

In Wittgenstein si tratta cioè soltanto di istituire un calcolo; ed eventualmente dei rapporti tra calcoli. E con ciò si comincia anche a intravvedere in che senso Wittgenstein tenderà più tardi a respingere l’idea di una «metamatematica» nell’accezione che Hilbert attribuisce a questa espressione.

5.

Che la filosofia della matematica del Tractatus si riduca ad uno spunto è interamente fuori questione. Del resto Wittgenstein stesso giudicherà più tardi che questa concezione, e in particolare quella del numero, era stata presentata nel Tractatus in una forma «nebulosa», «primitiva e insufficiente» [16]. Negare che essa contenga vari elementi interessanti, soprattutto se si tiene conto degli anni in cui queste idee vennero abbozzate, sarebbe invece una valutazione troppo superficiale.

Del resto la filosofia della matematica del Tractatus degna della massima attenzione anzitutto per ragioni interne ad una valutazione dell’opera e ad una sua precisa localizzazione. Che essa presenti un punto di vista non assimilabile a quello «logicista» è una cosa ovvia e che è spesso stata sottolineata. Ma è altrettanto ovvio, ed assai meno posto in rilievo, che si tratta di un punto di vista nettamente alternativo che non può né essere «recuperato» dentro un quadro logicista, né ricevere una valutazione adeguata a partire da esso.

Che su questo punto vi siano ancora larghi margini di equivocità dipende probabilmente dal fatto che sulle interpretazioni di Wittgenstein pesa ancora, per questo aspetto, la reinterpretazione e l’utilizzazione che Ramsey fece di alcune posizioni critiche centrali dell’opera. Nella sostanza, Ramsey mostrava che la concezione della «generalità» della logica sostenuta da Wittgenstein attraverso la nozione di tautologia introduceva nel programma logicista un tema di rilevante chiarificazione; e nello stesso tempo che le critiche particolari rivolte da Wittgenstein, come conseguenze dirette di quella concezione, al sistema assiomatico dei Principia, non solo non sembravano contrastare con quel programma, ma potevano essere accolte in esso e contribuire al suo miglioramento. Bisogna sottolineare allora l’originalità di Ramsey anche in rapporto a questo modo di utilizzazione; oltre che la coerenza con la quale egli espunge semplicemente l’intera filosofia della matematica del Tractatus. La critica di Ramsey prende le mosse dal tentativo di rendersi ragione della nozione di equazione in Wittgenstein avendo di mira quella di tautologia, e per così dire sovrapponendola ad essa. Ramsey non può assolutamente prendere in considerazione un’equazione senza vedere occhieggiare dietro di essa la proposizione. A dire di Ramsey, la matematica secondo Wittgenstein «consiste di proposizioni costruite, per mezzo di identità, mediante un processo analogo a quello secondo cui le proposizioni ordinarie si costruiscono con quelle atomiche; come dire che le proposizioni matematiche sono (secondo questa teoria) in un certo senso funzioni di verità di identità» [17].

Già da questo inizio appare chiaro che ci troviamo di fronte ad un fraintendimento radicale o, quanto meno, a punti di vista che sono semplicemente l’uno al di fuori dell’altro. E che dire poi se, seguendo l’ottica di Ramsey, arriviamo ad obiettare che la concezione della matematica di Wittgenstein è «evidentemente incompleta dal momento che vi sono anche ineguaglianze, più difficili da spiegare»?[18].

Quando Wittgenstein si richiama all’equazione come nozione «caratteristica» della matematica intende fare, come abbiamo visto, un discorso sulla matematica come algoritmo, traendo da ciò le conseguenze necessarie. Intende, in particolare, avviare un’impostazione che consideri 1’aspetto puramente linguistico, prescindendo da ogni considerazione esterna ad esso, e quindi anzitutto dall’uso significante di questo linguaggio. Alla base di ciò vi è la distinzione tra «proposizione» matematica e l’uso che di essa noi facciamo nella vita di ogni giorno, dove ci serviamo di essa «solo per concludere da proposizioni che non appartengono alla matematica ad altre che parimenti non appartengono ad essa» (6.211). Per Ramsey dobbiamo piuttosto, nell’interpretazione della nozione di equazione, lasciarci guidare dall’uso che le equazioni hanno «al di fuori della matematica, nelle proposizioni della vita quotidiana» [19].

Stando a Wittgenstein, noi non possiamo in alcun modo dire che la matematica consta di tautologie, perché non possiamo confondere nel quadro concettuale del Tractatus, l’una nozione con l’altra (Q, p. 112). Il punto della distinzione sta proprio nel fatto che la nozione di «funzione di verità» non svolge nessun ruolo nell’introduzione di quella di equazione.

Logica e matematica dovranno perciò essere in linea di principio distinte, benché ovunque nel Tractatus si faccia valere un punto di vista di stretta unità. Ovunque troviamo parallelismi e simmetrie espositive, nella posizione dei problemi e nelle proposte della loro soluzione. Ma in che senso possiamo dire, nel quadro del Tractatus, che la matematica è logica, che essa si riduce alla logica? Al più possiamo osservare che la matematica è un metodo logico (6.2) o, forse più precisamente, un metodo della logica (6.234) - ma con ciò affermiamo soltanto che le equazioni matematiche possono presentarsi nelle procedure inferenziali. Per il resto matematica e logica hanno questo in comune: esse sono calcoli. Da questo punto di vista va dato il massimo rilievo al modo in cui si pone il problema del numero, per quanto oscuro ed incerto sia l’abbozzo presentato da Wittgenstein. Di esso Ramsey non parla nemmeno. Quanto a Russell, egli si limita, nell’introduzione al Tractatus, ad un rapido cenno nel quale si osserva che la concezione presentata da Wittgenstein, oltre a richiedere una maggiore elaborazione tecnica, «così come si trova può venire solo applicata ai numeri finiti»; e che «nessuna logica si può considerare soddisfacente finché non si sia mostrata capace di trattare i numeri transfiniti». È vero che Russell aggiunge: «Non penso che nel sistema di Wittgenstein vi sia qualcosa che gli renda impossibile colmare questa lacuna». Ma che si tratti di un’espressione di pura cortesia, è mostrato se non altro dal fatto che egli abbandona l’argomento e prosegue, non senza ironia, osservando che l’atteggiamento di Wittgenstein nei confronti del misticismo è «più interessante che non tali questioni relativamente particolari» [20].

Naturalmente Russell ha ragione nel rilevare questo limite nella concezione del numero di Wittgenstein. L’infinità posta dalla nozione di operazione, l’infinità inerente all’iterazione dell’operazione è appunto l’infinità «potenziale». Rispetto a un impostazione metodica che acquisisce fin dai suoi primi passi una nozione di numero estensibile indifferentemente al finito ed all’infinito e che procede di conseguenza verso caratterizzazioni generalizzate delle operazioni aritmetiche, il radicale mutamento di punto di vista che Wittgenstein propone non poteva che essere considerato da Russell come un palese regresso, non meritevole nemmeno di una fugace riflessione.

D’altro lato non vi è dubbio che in Wittgenstein la giustificazione della nozione di numero in quella di operazione venga proposta in alternativa ad una giustificazione che comporti un rinvio alla nozione di insieme. L’affermazione di Wittgenstein secondo la quale «la teoria delle classi è affatto superflua nella matematica» (6.031) deve essere intesa come un’affermazione che vuole sottolineare, non tanto il carattere «fittizio» delle classi come entità, quanto piuttosto la svincolabilità della nozione di numero da quella di classe. E con ciò si viene a negare che un discorso sui nessi tra aritmetica e logica debba necessariamente passare attraverso la riduzione dell’aritmetica entro la teoria degli insiemi[21]. Ma questo è appunto l’intero programma logicista.

Note

[1] Wittgenstein sembra voler concretizzare questa idea in un’effettiva proposta notazionale (5.531, 5.532, 5.5321). Tuttavia ciò che importa qui è il modo in cui questo problema riceve il suo senso dalla sua stretta dipendenza dalla tematica generale del simbolismo.

[2] Wittgenstein und der Wiener Kreis, op. cit., pp. 242-3. Cfr. prop. 4.243 e 6.2322.

[3] Il termine «schema operativo» non è usato da Wittgenstein.

[4] In alcuni punti del Tractatus, Wittgenstein si serve in luogo di questo segno, del segno «/» che in Sheffer indica la «negazione alternativa».

[5] Tenendo conto del modo in cui Wittgenstein pone il problema, sarebbe perciò erroneo parlare dell’operatore in questione come operatore in cui può essere definita la negazione. Che si possa parlare della negazione come unico operatore primitivo, nel contesto del discorso di Wittgenstein, è ovviamente importante anche per ragioni di ordine generale. Le cose non muterebbero nella sostanza se con «N()» si intendesse la «negazione alternativa».

[6] Sull’interpretazione della notazione di Wittgenstein per la forma generale della proposizione, Russell fu il primo a confondere le cose spiegando nella Introduzione che tale simbolo significa «tutto quello che si può ottenere scegliendo delle proposizioni atomiche, negandole tutte, scegliendone poi alcune dal gruppo or ora ottenuto insieme con altre dal gruppo primitivo e così via, indefinitamente» (op. cit., p. 147). Black fornisce a sua volta questa stupida ricetta: «Prendiamo una scelta qualunque di proposizioni elementari e forniamo la congiunzione della negazione di ciascuna di esse; poi aggiungiamo questa proposizione all’insieme delle proposizioni elementari; prendiamo, da questo insieme ampliato, una scelta qualunque di proposizioni, neghiamole congiuntamente, aggiungiamo all’insieme la nuova proposizione, e continuiamo nello stesso modo» (Manuale per il Tractatus di Wittgenstein, op. cit., p. 303).

[7] Gli schemi qui indicati, insieme a quelli della loro negazione, presentano tutte le funzioni di verità di «p» e «q», ad eccezione della tautologia e della contraddizione. L’iterazione della procedura conduce a ulteriori proposizioni che saranno tautologie, contraddizioni o proposizioni già acquisite. Come è chiaro saranno possibili diversi ordinamenti seriali per le proposizioni generate, ed è interamente erroneo ritenere che sulla base del «termine generale» dovremmo saper determinare «esattamente quale sarebbe, poniamo, il centotreesimo termine delle funzioni di verità». Prendendo le mosse di qui, G. E. M. Anscombe ha scritto un capitolo tanto inutile quanto farraginoso su questo problema nella sua Introduzione al Tractatus di Wittgenstein, trad. it. a cura di E. Mistretta, Roma 1966, pp. 121-6.

[8] E non già, ad esempio «a e b e c, e niente altro». Questa integrazione, che riproporrebbe circolarmente la nozione «tutti», è resa superflua dall’assunzione della completezza della descrizione. Quando Wittgenstein sottoporrà a revisione questa posizione teorizzerà nello stesso tempo la possibilità della proposizione come immagine incompleta (Cfr. Wittgenstein und der Wiener Kreis, op. cit., p. 52).

[9] «Parole che designano forme.., sono indicazioni per la costruzione di un simbolismo» (Wittgenstein und der Wiener Kreis, op. cit., p. 220.

[10] Wittgenstein non dice nulla sul modo di pervenire dai numeri «interi positivi» (6.03) alle ulteriori estensioni. È probabile che pensasse ad una teoria generale delle operazioni e delle loro proprietà formali sufficientemente elaborata da consentire i passi ulteriori. Ad esempio, il passaggio più semplice per l’introduzione dei numeri interi negativi potrebbe essere compiuto introducendo la nozione di operazione inversa di un’operazione. Un’allusione in questa direzione potrebbe essere la prop. 5.528(a): «Un’operazione può revocare l’effetto di un’altra. Le operazioni possono elidersi l’un l’altra».

[11] Da un’osservazione come questa, se adeguatamente sviluppata ed articolata, si possono trarre le ragioni della posizione di Wittgenstein nei confronti della caratterizzazione della sede dei numeri in Frege e Russell (prop. 4.1252, 4.12721, 4.1273).

[12] L. Wittgenstein, Philosophische Grammatik, hrsg. von R. Rhees, Frankfurt a.M. 1969, p. 468.

[13] Cfr. ivi, p. 341.

[14] D. Hilbert e P. Bernays, Grundlagen der Mathematik, Berlin 1968, I, pp. 20-21.

[15] ivi, p. 22 e 24. (Nel testo le lettere a, b, c sono in caratteri gotici, essendo i caratteri latini riservati ad altro uso).

[16] Cfr. L. Wittgenstein, Philosophische Bemerkungen, hrsg. von R. Rhees, Frankfurt a.M.1964, p. 131 e OFM, II, 46.

[17] F.P. Ramsey, I fondamenti della matematica e altri scritti di logica, op. cit., p. 34.

[18] ivi, p. 300.

[19] ivi, p. 19.

[20] B. Russell, Introduzione al Tractatus, op. cit., p. 155. Fino a che punto sia stata fraintesa dalla critica la vera natura del contrasto teorico tra Wittgenstein e Russell, contrasto che ha nell’orientamento verso una fondazione ricorsiva dell’aritmetica in Wittgenstein uno dei suoi punti focali, è dimostrato non solo dal fatto che un simile orientamento è passato inosservato, facendo testo la liquidazione russelliana della filosofia della matematica del Tractatus, ma anche dallo scarso peso conferito al giudizio durissimo di Wittgenstein sull’Introduzione di Russell («Ma ora tu sarai in collera con me per quel che ti racconto: la tua Introduzione non viene stampata e quindi, probabilmente anche il mio libro. Quando mi trovai di fronte la traduzione tedesca dell’introduzione non potei decidermi a farla stampare con il mio lavoro. La finezza del tuo stile inglese infatti era - ovviamente - andata perduta nella traduzione, e ciò che restava era superficialità e fraintendimento [corsivo mio]. Ora ho inviato il trattato e la tua Introduzione a Reclam, cui ho scritto che l’Introduzione non voglio sia stampata, ma non gli deve servire che per orientarsi sul mio lavoro». RL, p. 255). Un simile gesto, di un autore sconosciuto nei confronti di una simile firma, non può affatto essere raccontato come un esempio di stravaganza.

[21] La motivazione che conduce Wittgenstein alla proposta di tagliare questo nodo sembra comunque essere, più che il dubbio sull’ammissibilità di totalità attualmente infinite di cose, la concezione della «generalità» della logica e della matematica. Potremmo dire, in breve, che, secondo Wittgenstein, che qui ha di mira soprattutto la posizione russelliana, l’accidentalità nella teoria del numero viene introdotta in questo modo di considerazione che, tenendo fermo il significato del segno numerico, fissa poi questo significato in rapporto all’insieme. Siamo allora in condizione di parlare di numeri solo se vi sono cose (Q, p. 97). E così si finisce con il non aver nulla da eccepire sul fatto che la non contraddittorietà dell’aritmetica possa dipendere da come è fatto il mondo, ad esempio dal numero dei suoi oggetti.

Capitolo III

Capitolo V