VI

Il passaggio al punto di vista del gioco

1.

In questo capitolo conclusivo vorremmo dare uno sguardo di scorcio ad alcuni temi generali delle Osservazioni sui fondamenti della matematica per mostrare che il nodo del passaggio dal primo al secondo Wittgenstein consiste essenzialmente in un apertura onnilaterale nella considerazione dei fenomeni linguistici che deve necessariamente passare attraverso la crisi dell’orizzonte ideologico del Tractatus e, nello stesso tempo, del suo esclusivismo teoretico.

Non siamo dunque di fronte ad una modificazione di interessi destinata a sfociare ed a fissarsi in una contrapposizione tra linguaggio della «scienza» e linguaggio della «vita quotidiana». Ciò che invece getta luce immediata su questa svolta è il passaggio - nei confronti del problema del linguaggio e quindi di tutte le questioni di ordine filosofico generale ad esso connesse - al punto di vista del gioco.

Nel Tractatus è ovunque predominante un punto di vista rigorosamente statico. Statica è in primo luogo la concezione complessiva del linguaggio: la logica deve rappresentare la sua struttura rigida ed immutabile così come rappresenta la struttura rigida ed immutabile del mondo.

In linea di principio vi è un unico linguaggio perché vi è una sola logica, dunque una sola forma di mondo. In stretta connessione con ciò, siamo disposti ad ammettere che vi siano momenti convenzionali nel linguaggio solo in quanto essi non arrivano a ciò che in esso vi è di essenziale; la pluralità dei linguaggi può essere concessa solo se può essere riaffermata la loro unità di principio.

In rapporto alla logica possiamo dire che processo e risultato sono equivalenti (6.1261) - cioè, che possiamo fare a meno del punto di vista del processo; e riaffermiamo l’«analiticità» delle proposizioni logiche anche nel senso in cui deve essere possibile «dare in anticipo una descrizione di tutte le proposizioni logiche «vere» (6.125). Nella logica «nessuna sorpresa» (6.1261).

A questa accentuazione potremmo forse contrapporre il «pensiero fondamentale» del Tractatus (4.63 12), il cui sviluppo conduce, tra le altre cose, alla tesi dell’irriducibilità delle «categorie» logiche alla nozione di oggetto ed alla posizione, in connessione ad esse, della tematica delle operazioni.

Tuttavia si tratta anche in questo caso di un momento di tensione dentro le polarità di cui è composta l’unità teoretica dell’opera. Come la soggettività, anche l’operazione deve alla fine ridursi ad una labile comparsa. Il mondo del Tractatus non consta di oggetti, fatti e operazioni. L’operazione si esprime nel suo risultato. Come operazione essa scompare: non è nulla fuori della sua cristallizzazione oggettiva.

La staticità che pervade questa concezione del mondo è strettamente connessa con quell’ideale di piena oggettività che guarda ambiguamente da due parti: dalla parte del linguaggio della scienza e dalla parte del silenzio mistico. Abbiamo già visto in che modo tutto ciò sia sotto la presa dell’ideologia.

E questa tonalità ideologica investe certamente anche il quadro generale entro cui si sviluppa la tematica del simbolismo, caricando di enfasi irragionevoli il nesso tra logica, linguaggio e mondo.

«Sì, il mio lavoro si è esteso dai fondamenti della logica all’essenza del mondo» (Q, p. 181).

Come potranno allora le nostre comunicazioni non ricevere il carattere di comunicazioni oracolari?

Il passaggio ad un punto di vista nuovo - ad un punto di vista in cui mettiamo in questione questo nesso, questa stabilità di strutture già date - ha come sua condizione la caduta di questo velo ideologico, di queste enfasi.

Ma in questa caduta deve anche coerentemente venire alla luce del giorno - con tutti i suoi problemi - il formalismo tendenziale e nascosto del Tractatus.

Le parole del linguaggio non sono più cifre che rinviano a nessi assoluti. Un linguaggio è un gioco. Niente altro che un gioco. Ed esso rivela tanto poco l’essenza del mondo quanto poco la rivela una normale partita a scacchi.

2.

Nella Grammatica filosofica si osserva ad un certo punto: «L’aritmetica è una sorta di geometria. Ciò che nella geometria sono le costruzioni sulla carta, nell’aritmetica sono i calcoli (sulla carta). Si potrebbe dire: essa è una geometria più generale» [1].

In fondo una simile affermazione poteva essere utilizzata anche per illustrare le idee del Tractatus, ed in particolare la parte che aveva, nel discorso di Wittgenstein, ciò che abbiamo voluto chiamare 1’intuizione del linguaggio. Ma la differenza del contesto sta in questo: nel Tractatus era la struttura logica della realtà a mostrarsi in questa intuizione; ora la posizione di questo rapporto appare profondamente immotivata.

Cominciamo, con l’intravvedere qualcosa in rapporto a questa svolta ed alla problematica che essa mette in questione, proprio prendendo le mosse di qui, da ciò che diventa ora il nostro richiamo all’evidenza dei calcoli.

Mettiamo allora senz’altro sotto gli occhi del lettore questo segno:

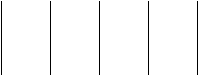
e notiamo che vi sono modi diversi di vederlo. Fra gli altri, questi:

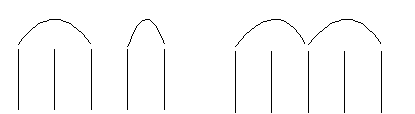
Che senso ha dunque affermare che la validità di una «proposizione» aritmetica può essere colta dal segno stesso poiché dipende dal modo in cui esso è fatto? Come è fatto un segno?

Dobbiamo tuttavia badare a non cadere nel facile equivoco che questa domanda suggerisce. Certo, qui facciamo notare che, se consideriamo un fatto percettivo come è la visione di una figura, dobbiamo comunque «presupporre» un qualche modo di vederla, un qualche schema di organizzazione dei suoi componenti figurali. Ma ricordiamo che già in precedenza ci siamo serviti di legature sovrapposte ai segni per illustrare il modo della loro costruzione operativa.

Questi piani non vanno confusi: una cosa è la struttura calcolistica di un segno, cioè il modo della sua costruzione in un calcolo, ed un’altra, interamente diversa, è il modo in cui esso si presenta alla percezione - la sua struttura percettiva. Non stiamo dunque attaccando il vecchio punto di vista come se la sua debolezza consistesse nel rinvio alla percezione come processo psicologico. Vogliamo piuttosto servirci di una similitudine: come nella visione di un segno si presuppone un qualche modo di vederlo, così nella considerazione della struttura di un segno in un calcolo si presuppongono le regole di un calcolo. Ma in questa similitudine non ci arrestiamo a questo punto. E non ci limitiamo nemmeno a sostenere che un segno, in un calcolo, è in ordine se è in ordine con le regole del calcolo. Il passaggio nuovo sta in questo: come vi può essere un calcolo nel quale cinque consta di tre e due, così vi può essere un calcolo in cui cinque consta di tre e tre.

Ma non ci imbattiamo a questo punto in una contraddizione? Dovremmo osservare: tra tutti i calcoli, ce ne deve essere uno in cui accade che le sue espressioni non solo sono in accordo con le regole del calcolo entro cui sono costruite, ma anche con le regole della logica - e da esso appunto una contraddizione deve essere esclusa.

Che una proposizione sia contraddittoria significa, poi, che essa non può avere nessuna applicazione, né nel nostro mondo né in nessun altro. Perciò potevamo dire, nel Tractatus, che la matematica mostra nelle equazioni quella «logica del mondo» che le proposizioni della logica mostrano nelle tautologie (6.22).

Ora cominciamo con l’osservare che possiamo perfettamente immaginare un mondo fatto in modo tale che in esso sia applicabile, ad esempio, l’equazione «3+3=5» - oppure «4x3+2=l0».

«Immagina che qualcuno sia stato stregato e perciò calcoli:

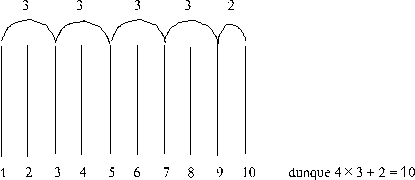
Ora deve applicare il suo calcolo. Prende quattro volte tre noci e poi ancora due noci e le divide tra dieci persone; e ciascuno ottiene una noce; perché egli spartisce le noci seguendo le legature del calcolo e, ogni volta che dà una seconda noce ad una persona, la noce sparisce» (I, 36).Qui ci viene proposto nient’altro che una fantasia. Noi supponiamo di essere stregati ed effettuiamo un calcolo strano.

Dopo di che fingiamo una situazione nella quale il risultato del nostro calcolo in qualche modo trova riscontro in una realtà nella quale scompaiono le noci. E scompaiono proprio in questo modo. Che cosa si intende mostrare con un simile modo di argomentare - al quale del resto dovremo abituarci? Si tratta intanto di cominciare con il suggerire che il calcolo non decide nulla sulla propria applicazione, al nostro mondo o ad un mondo che possiamo liberamente immaginare. Nell’esempio è importante proprio il fatto che si tratti di una fantasia. E comunque possibile che qualcuno sia stato stregato, e calcoli così. Ed è possibile che le noci scompaiano e scompaiano proprio in questo modo.

Perché mai le noci non dovrebbero scomparire?

3.

Tra i nostri giochi, ve ne sono alcuni che hanno a che fare con problemi di composizione e scomposizione di figure. Ad esempio, ci viene proposto di formare un rettangolo con questi triangoli (I, 42):

Tutti sappiamo quali sono le diverse situazioni che si possono presentare.

Può accadere che il compito venga eseguito con estrema facilità. Vediamo subito in quei pezzi la possibilità della

forma rettangolare. E passiamo senz’altro all’esecuzione del compito proposto. Ma in realtà non è del tutto semplice spiegare chiaramente che cosa sia successo qui. Che cosa abbiamo effettivamente visto? Se si tratta del rettangolo, allora abbiamo visto qualcosa che certo non abbiamo di fronte agli occhi. Qui ci sono solo i triangoli. Potremmo spiegarci osservando: la forma rettangolare l’abbiamo vista attraverso questi triangoli che sono sotto i nostri occhi. Ma non è forse imbarazzante doversi esprimere così? Che cosa significa mai «vedere attraverso» le figure?

Supponiamo invece che questo compito venga risolto con qualche difficoltà. Cioè: effettuiamo alcuni tentativi, alcuni esperimenti di costruzione. Sappiamo che alla fine dobbiamo giungere alla forma rettangolare. Ora proviamo ad accostare le figure in questo modo, poi in quest’altro e intanto ci pensiamo sopra. Alla fine ci riusciamo.

Come spiegare in che modo sono riuscito a costruire la figura? All’inizio ho effettuato dei tentativi abbastanza casuali. Non potevo che cominciare così, casualmente, perché il rettangolo, in realtà, non lo vedevo affatto. Ho effettuato perciò una prima composizione - eventualmente utilizzando due pezzi soltanto. Poi ci pensavo sopra. O meglio: non pensavo affatto. A che cosa mai avrei dovuto pensare?

In realtà guardavo intensamente la figura, concentravo il mio sguardo su di essa per vedere sorgere attraverso di essa il fantasma del rettangolo.

Del resto, non è che io pensi di costruire il rettangolo pezzo a pezzo, provando e riprovando. Non si tratta di una costruzione graduale perché in tal caso di fronte ai miei occhi vi dovrebbe già essere la forma rettangolare, che continuo a non vedere. Dunque opero accostamenti casuali. Non ho altra scelta. E tuttavia non è che io pensi di venire a capo del problema in modo casuale - come se eseguissi il gioco ad occhi chiusi. Ma perché in questo modo, operando questo e quest’altro accostamento, con questi movimenti dei pezzi, li propongo ad una considerazione da lati diversi, li considero sotto aspetti diversi. La difficoltà di questi giochi sta appunto in questo; io guardo i triangoli e rimango bloccato da un certo loro aspetto, non riesco a vederli in altro modo che così, non riesco a vedere in essi quella possibilità di combinazione.

Operando accostamenti parziali cerchiamo di vincere questo blocco. Questi tentativi di costruzione servono soltanto ad aprire quella prospettiva, a liberare una nuova piega dello sguardo, a vedere attraverso le figure ciò che ora non riesco assolutamente a vedere. Ma anche questo è strano: è strano pretendere di vedere questi triangoli in un modo diverso: questi triangoli sono quelli che sono.

La situazione più sconcertante è quella in cui il gioco non riesce. Non solo non vediamo come combinare i pezzi per formare la figura, ma ogni tentativo di proporre costruzioni parziali, ogni tensione dello sguardo per cogliere gli aspetti che indirizzano verso la forma fallisce. Eppure sappiamo che la soluzione del gioco deve essere estremamente elementare, che essa è anzi a portata di mano: solo che non vediamo la strada. «Un demone ha lanciato un incantesimo su questa posizione e l’ha esclusa dal nostro spazio» (I, 45). È come se vi fosse un punto cieco nel nostro cervello (I, 44). Ma potremmo anche arrivare a concludere: abbiamo provato e riprovato in mille modi. Con questi pezzi non si può formare un rettangolo. Ora sappiamo che non si può. Che dire poi se ci viene provato che si può con l’esibizione di questa figura?

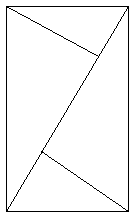
Ora vediamo che ciò che ritenevamo impossibile è invece possibile. Di questo ci sorprendiamo. La prova ci sorprende (I, 69).

Del resto potremmo anche non darci per intesi di fronte alla prova. Certo ora vediamo un rettangolo - ma le figure di cui esso è composto non sono più quelle di prima. Sono cambiate. Queste infatti combaciano così, quelle di prima no. Ed in che modo è possibile che esse siano cambiate? Ad esempio, per un atto di magia, per un gioco di prestigio. Le figure si combinano ora in questa forma «ma per un trucco, per una disposizione contorta, in modo innaturale». Un bambino potrebbe anche reagire così (I, 50).

Qualcosa di simile ad un discorso comincia a dipanarsi in questa forma allusiva e metaforizzante. Una prova mostra anzitutto una nuova possibilità, «cambia la tua geometria», «ti indica, per così dire, una nuova dimensione dello spazio» (I, 44). Mostra un modo diverso di vedere le cose, un aspetto che non eravamo riusciti a cogliere. Ad esempio, non avevamo visto che tutto il problema consisteva nel ribaltare il pezzo, non avevamo visto in quel triangolo la sua immagine speculare (I, 49).

D’altro lato, è sempre possibile trovare un modo per rifiutare la prova. In che senso abbiamo mostrato, esibendo la figura, la possibilità di quella combinazione? Dobbiamo dire che la prova esclude ogni dubbio sulla possibilità di questo modo di composizione e scomposizione, che essa porta alla luce questa possibilità di scomposizione del rettangolo come una sua «proprietà essenziale», che la prova ci assicura di questo una volta per tutte e che essa può essere rifiutata appunto soltanto con argomenti infantili?

Si ammetterà, ad esempio, che cinque consta di tre e due:

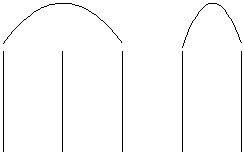
Ma che cosa significa ammettere questo e ammetterlo sulla base di questa figura (I, 53)?

In realtà, potremmo subito accingerci a sollevare dubbi di vario genere. Ogni dubbio invece sarebbe tolto se, rinunciando all’affermazione che la prova in se stessa mostra una proprietà essenziale della figura, stabilissimo come regola che un gruppo è una figura-cinque solo se può essere scomposto in una figura-tre e in una figura-due (I, 67).

Voglio ammettere dunque che cinque consta di tre e due «solo se, così facendo, non ammetto nulla. Se non che, voglio impiegare questa immagine» (I, 53).

4.

Alla «sorpresa di fronte alla prova» possiamo contrappone l’affermazione del Tractatus secondo la quale nella logica «non possono mai esserci sorprese» (6.1252). Naturalmente, nel Tractatus, con ciò vogliamo soltanto caratterizzare una certa nozione del calcolo - il fatto che si parli di «sorpresa» non contiene nessun rinvio a qualche aspetto psicologico. Ma la stessa cosa potremmo affermare anche in rapporto alla «sorpresa di fronte alla prova», dove si tratta appunto di caratterizzare una nozione diversa. In generale, se si osservasse che il nostro modo di avvio dalla composizione e scomposizione di figure sarebbe fin dall’inizio compromesso in una direzione psicologistica, dovremmo semplicemente far notare che ciò che viene proposto, negli esempi di costruzione delle figure, sono appunto giochi, e non problemi geometrici (o aritmetici).

Anche l’esempio delle «cento palline» (I, 36), di cui ci vogliamo ora occupare, può essere introdotto sullo sfondo di un’altra frase del Tractatus: «Il calcolo non è un esperimento» (6.2331(b)).

Poiché nel Tractatus logica e matematica sono considerati in ultima analisi sulla base della nozione del calcolo, e poiché dalle espressioni dell’una e dell’altra distinguiamo le proposizioni che hanno contenuto empirico, quella frase richiama ancora una volta la distinzione cardinale tra sfera apriorica e sfera empirica. Lo stesso termine di «calcolo» può essere usato come un titolo dell’a priori: ed allora diciamo che dai calcoli distinguiamo nettamente gli «esperimenti».

Sarebbe un grave errore ritenere che ora questa distinzione venga meno. E indubbio anzi che questa differenza venga riproposta con eguale nettezza. Ciò che invece diventa problematico è in che modo essa debba essere fissata in un quadro generale nel quale non possiamo più contare su una delimitazione determinata e definita dello «spazio logico», sull’unicità e l’assolutezza delle strutture logiche, e quindi linguistiche, di determinazione della realtà.

Nell’esempio delle «cento palline» abbiamo a che fare con un tale che dispone su un tavolo, schierate in una fila, cento palline, e che fa certe cose con esse. Noi siamo gli osservatori del suo comportamento. Se egli faccia un gioco o qualcos’altro non lo sappiamo esattamente.

A partire dalla posizione iniziale, egli opera nuovi schieramenti. Ad esempio, lascia uno spazio vuoto più ampio ogni dieci palline. Quindi ogni gruppo di dieci viene separato in modo analogo in due gruppi di cinque palline. Infine le palline vengono incolonnate, disponendo ogni fila di dieci l’una sull’altra, separando poi con uno spazio vuoto più ampio le prime cinque file dalle rimanenti, e così via.

Se di fronte a queste evoluzioni ci viene in mente il nostro familiare pallottoliere, osserveremo probabilmente: in questo modo ci viene mostrata «la parte che 100 ha nel nostro sistema di calcolo» (I, 81). Ma questa non è che una nostra congettura. Può essere che si vogliano mostrare altre Cose, e molto diverse.

Ad esempio, che queste palline non sono incollate le une alle altre o sul piano sul quale si trovano. Oppure che nessuna di esse, spostandole in questo modo, scompare (come potrebbe accadere) (I, 75).

Nel primo caso si tratterà di un calcolo, negli altri di «esperimenti».Ma l’esempio mostra appunto che la situazione del calcolo o dell’esperimento può inizialmente essere indistinta rispetto all’una o all’altra «interpretazione»,

In entrambi i casi abbiamo a che fare con cose concrete, provviste di caratteristiche fisiche ben determinate, che manipoliamo in vari modi. Nel caso di un «esperimento», tuttavia, vogliamo proprio mostrare che queste cose qui hanno queste e queste altre proprietà. Mentre di fronte ad un bambino che, ad esempio, si rifiutasse di accettare che ciò che viene mostrato in rapporto a queste palline possa valere senz’altro per le altre cose - e addirittura per le altre palline - dovremmo cercare in qualche modo di sopprimere ciò che in questa situazione vi è di «sperimentale» - cioè, i momenti che rinviano alla concretezza.

Forse potremmo cominciare con lo spiegarci riprendendo ciò che abbiamo fatto con una macchina da presa e senza mettere a fuoco l’obiettivo, cosicché nella proiezione abbiamo a che fare con delle macchie di colore senza sapere esattamente che cosa rappresentino. «Ebbene, sullo schermo non vedo certo un esperimento. Ma ciò che in questo procedimento vi è di »matematicamente essenziale« lo vedo anche nella proiezione! Anche qui infatti, prima compaiono cento macchie, poi queste macchie vengono divise in gruppi di dieci, ecc. Potrei dire dunque: la prova non mi serve da esperimento, ma da immagine di un esperimento» (I, 36). «La prova - si potrebbe dire - deve essere originariamente una specie di esperimento, ma poi la si prende semplicemente come immagine» (II, 23).

È certo comunque che resta ancora una connessione con la concretezza. Qui si tratta di imprimere una certa immagine e per questo dobbiamo, per così dire, scegliere il materiale adatto (I, 37).

5.

Le varie cose che dice Wittgenstein facendo riferimento alle figure:

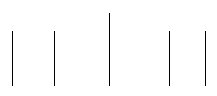
A.

B.

potrebbero essere dette altrettanto bene facendo uso di figure che ci sono più familiari: quadrati e rettangoli, ad esempio. Credo tuttavia che ci sia una precisa ragione che spiega questa stravaganza. Potremmo infatti considerare queste figure come se le vedessimo qui per la prima volta. In certo modo ci troviamo in una situazione simile a quella delle acquisizioni iniziali, dell’addestramento elementare.

Qual è il problema che viene ora sul tappeto? La prova è una figura, ma una figura in se stessa non è una prova. Se tiriamo linee dai segmenti della figura A ai vertici della figura B per provare che la prima ha tanti segmenti quanti sono i vertici della seconda, otteniamo la figura:

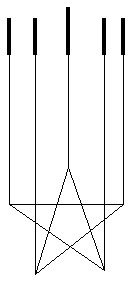
E questa è appunto una figura come tutte le altre: ciò che vediamo è una «stella con appendici filiformi» (I, 25). Non sappiamo affatto di che cosa dovremmo convincerci guardandola. Del resto in rapporto alla prova di certe proprietà del numero cento mostrate con la fila delle cento palline avremmo potuto dire: «Ciò che tu hai reso manifesto è proprio la fila delle cento palline» (I, 75).

Possiamo forse ottenere qualche utile suggerimento in rapporto a questo problema se consideriamo i primi passi verso l’acquisizione di una «forma». Perciò ha il suo peso il fatto che ci vengano proposte figure «inventate», cioè figure che non hanno posto tra le figure della geometria così come ci è stata insegnata a scuola. Possiamo supporre che, per un bambino, un «pentacolo» - come chiamiamo la figura B - o una «mano» - come chiamiamo la figura A -sarebbero familiari non più e non meno dei quadrati o dei rettangoli che il maestro gli mostra quando li disegna per la prima volta alla lavagna.

Notiamo allora soltanto due cose: il maestro, con il solo fatto di disegnare una certa figura alla lavagna (aggiunto al fatto che egli è, appunto, il maestro) «attira l’attenzione» su di essa, apre cioè nei suoi scolari la disponibilità ad attribuire a quella figura, tra tutte le altre, una posizione in certo modo privilegiata, quindi ad .accettare che essa abbia proprietà particolarmente «degne di interesse» (e ciò accadrebbe anche se egli disegnasse, in luogo del quadrato, una stella a cinque punte).

Quanto al quadrato poi, un maestro elementare lo disegnerà alla lavagna - probabilmente - non in un modo qualsiasi, ma nel modo più naturale, ad esempio, non certo così:

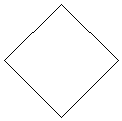
Lo disegnerà, cioè, in un modo tale che la figura si imprima facilmente nella mente - come appunto fa Wittgenstein con il suo «pentacolo»: «L’ho disegnato apposta in modo che rimanga facilmente impresso» (I, 25).

In questo processo di fissazione di una forma che così ha inizio, un passaggio essenziale viene effettuato nel momento in cui puntiamo il dito sulla figura e diciamo: questa figura si chiama... E poi ancora: ora disegnate un...

«Quale era il senso della nostra proposta di dare un nome alle cinque lineette parallele e alla stella a cinque punte? Che cosa è accaduto per il fatto che hanno un nome? Si sono date certe indicazioni sul modo di uso di queste figure. Cioè - ora le si riconosce al primo colpo come questa e quella figura. Adesso non si contano più i loro segmenti o i loro angoli. Per noi sono configurazioni tipiche, come coltello e forchetta, come lettere e cifre» (I, 41).

Perciò al comando: «Disegna un pentacolo!», «io posso riprodurre immediatamente questa forma» (I, 41).

E poi proseguiamo, ad esempio, mostrando mediante una prova che un pentacolo ha tanti vertici quanti sono i segmenti dì una mano - che questa relazione tra pentacoli e mani è, per usare la terminologia di una volta, una relazione interna: non può darsi il caso che si dia una figura del tipo A e una figura del tipo B e non sussista tra loro questa relazione.

Dovremmo dire allora che la «stella con appendici filiformi» porta alla luce una proprietà essenziale delle figure? Che la prova «indaga sull’essenza» (I, 32)?

In realtà noi avremmo potuto anche non attirare l’attenzione proprio su queste figure, avremmo anche potuto non dare ad esse nessuna importanza nella nostra geometria. Oppure, in ogni caso, avremmo potuto sviluppare i nostri discorsi in tutt’altra direzione, avremmo potuto ritenere una proprietà come questa irrilevante e del tutto priva di interesse.

La prova dunque non «indaga sull’essenza», ma la fissa e la circoscrive. È essa che opera questa discriminazione tra ciò che deve essere considerato essenziale e ciò che deve essere considerato inessenziale. «Perché ora considero una cosa come del tutto ovvia, ora invece la trovo degna di nota» (I, 85).

«Oppure anche: la prova non indaga sull’essenza delle figure, ma esprime quello che, d’ora in poi, dovrò considerare come appartenente alla loro essenza» (I, 32).

Presentare una prova significa propone un’immagine per una valutazione. Ed accettare una prova, dunque, decidere di impiegare questa immagine.

Così se nella ripetizione della prova dovesse accadere che non si dia tra le nostre figure quella relazione concludo: devo aver sbagliato qualcosa. Non può essere così. Forse mi sono dimenticato di tirare una linea. Come quando di fronte a due e due mele che fanno tre mele concludo: «In un modo o nell’altro deve essere sparita una mela» (I, 156).

6.

Finora ci siamo mossi, un po’ a fatica, in mezzo a situazioni analogiche, vaghe allusioni, suggerimenti e suggestioni. Tuttavia, nonostante tutto, nonostante il fatto che saremmo tentati di sottrarci senz’altro alle costrizioni a cui ci sottopone una simile forma di esposizione, forse potremmo arrivare ad ammettere che le linee della nuova impostazione teoretica cominciano con il prendere un chiaro rilievo. Esse convergono verso una radicale messa in questione dell’interpretazione della nozione di conseguenza logica che avevamo dato ai tempi del Tractatus.

Da certe proposizioni, che chiamiamo premesse, viene tratta una proposizione - la conclusione - in conformità con certe regole deduttive. Nella cornice del Tractatus si ribadiva con insistenza l’idea che le regole deduttive non fanno altro che presentare certi schemi di rapporti strutturali tra le proposizioni. In questo senso esse sono «superflue»: la possibilità che tra certe proposizioni sussista un rapporto di conseguenza è fondata nella struttura delle proposizioni stesse. Un altro modo di esprimere questa stessa idea potrebbe essere: la dimostrazione non fa altro che rendere esplicita quella conclusione che in ogni caso è contenuta nelle premesse: essa «segue già - io non devo fare altro che inferirla» (I, 21).

Ma ora questa frase è messa in bocca da Wittgenstein al proprio «interlocutore interno», che assume, in questa occasione, le vesti del logico «logicista».

Di fronte a ciò sono gli argomenti formalisti che vengono in primo piano.

Una dimostrazione è un «disegno ornamentale» (I, 18) (come la stella con appendici filiformi).

Si sarebbe subito tentati di obiettare, prima ancora di proseguire oltre: nessun dubbio che una dimostrazione possa essere considerata unicamente come una sequenza di segni, prescindendo dalla concatenazione dei pensieri che in essa si esprime. Ma se questa sequenza deve essere poi interpretata come una dimostrazione è necessario che il passaggio da segno a segno possa esprimere appunto il passaggio, logicamente necessario, da un pensiero ad un altro pensiero.

Chiediamo allora che cosa si debba intendere con questo passaggio, con l’inferire inteso in questo modo. Certamente non «un’attività del tutto particolare, un processo che avviene nel mezzo del nostro intelletto - qualcosa di simile ad un ribollire di vapori dal quale poi balza fuori la conclusione» (I, 6).

Ma che cosa allora? «C’è un passaggio da una proposizione all’altra tramite altre proposizioni, e dunque attraverso una catena di inferenze; ma di questo passaggio non c’è bisogno di parlare, perché presuppone un altro tipo di passaggio, vale a dire quello da un anello della catena all’anello successivo. Ora, tra due anelli della catena può aver luogo un processo di transizione, ma neppure in questo processo non c’è nulla di misterioso, perché esso consiste nel derivare un segno proposizionale da un altro in conformità con una regola, nel paragonare entrambi questi segni ad un paradigma che per noi rappresenta lo schema del passaggio - o in altre cose dei genere. Questo può avvenire sulla carta, nel discorso orale o ’nella nostra testa’; ma la conclusione si può anche trarre enunciando una proposizione dopo l’altra, senza compiere il trapasso, oppure il trapasso consiste solo nel fatto che si pronunciano espressioni come ’dunque’, ’di qui segue...’, eccetera. In questo caso la proposizione inferita si chiama ’conclusione’ perché si può di fatto derivare dalla premessa» (1,6).

Osserviamo, cioè, che se escludiamo, come sembra giusto fare, che il processo dell’inferire sia da intendere come qualcosa di psicologico, allora non ci è affatto chiaro in quale altro modo esso debba essere inteso, mentre ci è perfettamente chiaro che nell’inferire non facciamo altro che «paragonare entrambi questi segni ad un paradigma che rappresenta per noi lo schema del passaggio».

L’obiezione precedente può essere allora ribadita e rafforzata. Ritenere che dalla possibilità di un’effettuazione «meccanica» della deduzione nella quale ci si attiene appunto soltanto al momento formale, sia senz’altro lecito recidere nettamente il nodo che connette queste regole dei segni alla legalità logica ed alla sua necessità, significa colpire la stessa nozione di conseguenza logica, poiché le si sottrae quel terreno di oggettività nel quale essa deve essere radicata; significa negare un fondamento «reale» della logica, ridurre le leggi logiche a norme che possono non solo essere misconosciute, ma anche legittimamente trasgredite; e rinunciare dunque alla posizione della discriminazione tra inferenza corretta ed inferenza scorretta come una discriminazione oggettiva.

È chiaro allora che questa obiezione non rappresenta per noi affatto un’obiezione, che anzi il suo contenuto lo possiamo fare interamente nostro.

Adottare il punto di vista del gioco significa sostenere anzitutto che vi è una molteplicità di giochi linguistici. E perciò anche che non vi sono inferenze corrette e scorrette che siano tali in se stesse, e quindi in rapporto ad ogni linguaggio.

Con le sue leggi fondamentali della logica «Russell vuol certamente dire: d’ora in poi inferirò in questo modo, e pertanto esso dovrà considerarsi corretto» (I, 20). Attraverso la loro posizione non si fa altro che fissare il tipo di successioni di segni proposizionali che si presenteranno in questo libro a titolo di dimostrazioni: con l’importante precisazione che si tratta di questo libro, nella misura in cui «anche leggere questo libro fa parte di un gioco che deve essere appreso» (I, 18).

A questo punto potremmo muovere una seconda obiezione: se adottiamo in rapporto a questo problema il punto di vista secondo il quale si tratta, nella dimostrazione, sol tanto di paragonare i segni proposizionali ad un paradigma che «rappresenta per noi lo schema del passaggio» sembrerebbe in tal caso che l’accertamento del sussistere di un rapporto di conseguenza debba ridursi ad un accertamento di ordine empirico. Non solo sarebbe inevitabile una relativizzazione della nozione di conseguenza logica, ma anche una sua psicologizzazione.

«‘Quando guardi questa catena di trasformazioni, non ti sembra anche che esse concordino con i paradigmi?’» (I, 157). «Se dunque questo si deve chiamare esperimento, allora sarà sicuramente un esperimento psicologico. L’apparenza dell’accordo può benissimo riposare su un’illusione dei sensi. E quando facciamo un errore di calcolo qualche volta è proprio così. Si dice anche: ’Mi risulta questa cosa’. E senza dubbio questo è un esperimento, il quale mostra che questa cosa risulta a me» (I, 158).

Dobbiamo dunque ammettere che l’adozione del punto di vista del gioco comporti senz’altro una concezione esplicita o implicita di carattere psicologistico, quindi, seconde la terminologia di Wittgenstein, la soppressione della differenza tra «calcolo» ed «esperimento»? In realtà questa distinzione viene ribadita anche a questo punto: «Non confondere i sentimenti (gesti) di concordanza con quello che fai con la prova!» (I, 24).« Quando si concepisce una prova come risultato di un esperimento, il risultato dell’esperimento e ciò che si chiama risultato della prova non sono in nessun caso la stessa cosa. Il risultato del calcolo è la proposizione con la quale si conclude, il risultato dell’esperimento è: che da queste regole sono stato condotto a questa proposizione» (I, 161).

7.

Nel dare rilievo alle argomentazioni formaliste non si trattava certo di scindere il nesso tra linguaggio e pensiero, ma piuttosto di aprire la prospettiva di una legalità dinamica del pensiero, indicando nel riconoscimento della possibilità di linguaggi essenzialmente diversi la sua condizione prioritaria.

Alla posizione implicita nell’affermazione: «‘Se pensi non puoi non ammettere questa prova’» (I, 51), contrapponiamo che a questa cosa è una dimostrazione solo per chi la riconosce come tale, chi non la segue come si segue una dimostrazione si trova su un piano diverso dal nostro ancora prima che si cominci a parlarne» (I, 61).

Respingiamo perciò come falsa l’alternativa tra una nozione di razionalità oggettivamente fondata e la soppressione di ogni razionalità nei dati di fatto psicologici o antropologici; e cerchiamo di teorizzare, ad un tempo, l’insussistenza di un unico campo di idealità che hanno valore normativo assoluto e la possibilità dell’assunzione paradigmatica di schemi di valutazione.

Per questo può accadere che ci si esprima qualche volta come «platonici» nel contesto di un «antiplatonismo» polemico ed aggressivo. Nello spirito del platonismo descriviamo la «forma» come un sottile disegno, come una sottile intelaiatura sulla quale vengono modellate le cose che hanno questa forma (I, 72). Oppure diciamo che le proprietà essenziali della forma «sussistono sempre e inesorabilmente nella totalità che istituiscono; sono per così dire indipendenti da tutti gli accadimenti esterni. Allo stesso modo i piani di costruzione di una macchina tracciati sulla carta non vanno distrutti quando la macchina soccombe all’azione di forte esterne. Oppure vorrei dire: sono sottratte al vento ed alle intemperie, come ciò che vi è di fisico nelle cose, ma sono inattaccabili come spettri» (I, 102).

Nello stesso tempo, ogni pretesa di necessità, di evidenza, di «inesorabilità» viene contrastata e contestata con argomenti che non intendono arrestarsi di fronte a nulla.

«Non è già un buon esempio l’inesorabilità con cui due segue ad uno, tre a due, e così via?» (I, 4).

Dovremmo parlare piuttosto della «spietata esattezza», dell’«esercizio infinito» con il quale veniamo addestrati a questa successione. E veniamo addestrati in questo modo per via dell’importanza che questa successione ha nel nostro mondo: «il contare e il fare calcoli non sono semplici passatempi» (I, 4).

Una posizione che viene ribadita nelle forme più varie, fino alle ben note negazioni estreme:

«Ma allora, in una catena di inferenze non sono costretto a procedere come procedo? - Costretto? Ma io procedo come voglio!... Puoi indicarmi tutte le regole che vuoi - io ti indicherò una regola che giustifica il mio impiego delle tue regole» (I, 113).

«‘Però tu ora non puoi improvvisamente applicare la legge in modo diverso!’... Ma se io rispondessi semplicemente:‘In modo diverso? Ma non è affatto diverso!’ Che cosa faresti tu? In altre parole: uno può ancora rispondere come un essere razionale e tuttavia non giocare il nostro gioco» (I, 115).

Non esitiamo dunque ad imboccare la china che conduce ad un soggettivismo estremo cui il nostro interlocutore «platonico» ci sospinge. Si tratta tuttavia essenzialmente di una provocazione. In effetti quanto più accentuiamo questo momento soggettivo-individuale, secondo una tonalità che ha anche un’ovvia valenza etica, tanto più assume rilievo il fatto che talora possiamo constatare un «grande e interessante accordo», che vi è comunque una tendenza a «precipitarsi per raggiungere un punto di accordo comune a tutti» (II, 69).

Se vogliamo usare il termine di «convenzionalismo» per caratterizzare la posizione di Wittgenstein dobbiamo sottolineare che «convenire» significa anzitutto «incontrarsi». Ed in questo senso possiamo parlare di un profondo bisogno della convenzione. In esso dobbiamo ricercare il senso effettivo del profondo bisogno dell’essenza (I, 74)

Nella vita non ci possiamo muovere alla cieca. Ci è necessaria una strada. Ed i paradigmi sui quali conveniamo con altri fanno appunto questo: determinano un contesto, istituiscono ed anticipano una struttura, un modo di organizzazione. L’immagine della strada - che è certamente un immagine intersoggettiva - diventa una sorta di modulo stilistico che ricorre più volte nei discorsi di Wittgenstein, e spesso in contesti nei quali di fronte al tema di una libertà nel vuoto che disorienta si presenta l’istanza di contrassegni di un possibile cammino.

Fin dall’inizio siamo avviati su una strada: tutto ciò che apprendiamo nei primi anni della nostra infanzia è l’indicazione di una strada che è già stata a lungo percorsa. Anche noi la percorriamo: poi può accadere di trovare una strada diversa: «e adesso il traffico si svolge su questa strada, verso mète differenti» (I, 162).

Diciamo con ciò che i paradigmi, gli schemi di valutazione sono giustificati e fondati nella convenzione? Che quindi, il carattere necessitante delle regole sarebbe legato alla stabilità delle istituzioni umane?

Certamente no. Un «paradigma» non è tale per il fatto che vi è un accordo sul suo uso. Accade spesso che Wittgenstein osservi: di fatto noi ci comportiamo così (ed altri si comportano o potrebbero comportarsi in modo diverso). Se volessimo andare alla ricerca di una spiegazione del dato di fatto di questo accordo è molto probabile che si debbano prendere in considerazione le forme di vita degli uomini che si comportano così - che il linguaggio stesso debba essere considerato non solo in se stesso come un gioco, ma come momento di un gioco di cui esso assolve solo una parte, l’altra invece è assolta da coloro che del linguaggio si servono.

Ma in ogni caso, sull’accordo, sulla convenzione, poggia non già il paradigma, ma il suo impiego.

Anche per Wittgenstein, come per il suo interlocutore «platonico» i paradigmi sussistono in questo modo: «inattaccabili come spettri» (I, 102).

Ed il linguaggio resta un titolo dell’a priori. Nonostante il rovesciamento dell’impostazione di principio del Tractatus, ripetiamo che vi è un senso in cui possiamo affermare che la logica e la matematica fanno tutt’uno, che entrambe appartengono all’ambito dell’apriori: l’una e l’altra si muovono infatti tra le regole del linguaggio. È questo che conferisce ad esse la loro «particolare solidità», la loro posizione «inattaccabile e solitaria» (I, 164).

La novità del contesto sta invece tutta nella formula famosa, che può essere così facilmente fraintesa: «Il matematico non scopre: inventa» (I, 167).

Il «matematico» - e siamo qui in fondo liberi di intendere questa parola in un senso anche molto esteso - presenta immagini, mostra in che modo sia ora possibile ciò che prima ritenevamo impossibile: «apre al traffico strade sempre nuove, estendendo la rete di quelle vecchie» (I, 165). In qualche modo egli è simile ad un architetto. Questi progetta case e giardini, e ciò corrisponde ad un bisogno reale della vita - il bisogno di una casa, ed anche di un giardino. Ma può ben darsi che egli si limiti a disegnare sul foglio sentieri per un giardino «come disegni ornamentali senza affatto pensare che un giorno qualcuno potrà camminare per essi» (I, 166). Potremmo dire: per un «bisogno estetico». Ma certamente diremmo meglio: per gioco, cioè: senza pensare ad un’applicazione.

8.

Parlare di invenzione matematica, di «creatività» del fare matematico, di produzione di essenze (I, 32), e così via; o anche, paragonare il matematico ad un architetto che disegna sentieri (piuttosto che ad un geografo che descrive un continente) sono in realtà frasi vuote se non vengono connesse non solo ad una concezione della matematica caratterizzata dal rinvio alla nozione del calcolo, ma anche ad una determinata interpretazione di questa nozione.

Come abbiamo osservato or ora, nell’affermazione che la matematica si muove tra le regole del linguaggio vi è un richiamo alle concezioni del Tractatus, sia perché risulta così ribadita la distinzione tra la «proposizione» matematica, che ha appunto la «dignità di una regola», e le proposizioni empiriche, che sono invece constatazioni di fatti; sia perché in questa formulazione si dice solo in modo diverso che «la matematica consta di equazioni» - dove l’equazione si presenta come nozione fondamentale solo in quanto in riferimento ad essa possiamo illustrare nel modo più elementare la nozione di «calcolo».

L’aspetto nuovo sta nel fatto che non possiamo più intendere le «equazioni» come espedienti «puramente» tecnici, che hanno il solo scopo di ottenere una semplificazione del simbolismo. Certamente, potremo sottolineare 1’ importanza di simili espedienti anche se in essi non vedessimo nulla più di regole per l’introduzione di «abbreviazioni»: ad esempio, in luogo del numero cento scritto mediante una sequenza di tratti, scriviamo, in base ad una regola, il numero cento nella nostra usuale notazione decimale. Da un certo metodo notazionale passiamo ad un altro metodo notazionale, i cui vantaggi rispetto al precedente non hanno nemmeno bisogno di essere illustrati. E tuttavia non è facile intravvedere qui qualcosa di simile ad un’invenzione matematica che investa, per così dire, anche la sfera dell’«elaborazione concettuale». L’importanza che possiamo attribuire alle definizioni resta comunque un importanza pratica: dal punto di vista «logico» esse non sono affatto importanti. Questa era la tesi dominante nel Tractatus: da un lato si sosteneva la centralità della nozione di equazione come regola di sostituzione, dall’altro, e proprio per il fatto che essa non fa altro che introdurre nuovi «segni» per gli stessi «simboli» (come dicevamo allora) si sosteneva nello stesso tempo la sua «inessenzialità» logica.

La strada che ora vogliamo seguire procede nella direzione opposta: mediante una definizione si introducono nuovi concetti. E «chi ha inventato il calcolo nella notazione decimale ha fatto una scoperta matematica» (II, 46).

Per illustrare brevemente questo punto, ci serviremo di un esempio molto semplice e chiaro proposto da Wittgenstein (II, 47).

Con la definizione: «a₁´a₂´...´a_n=aⁿ» introduciamo anzitutto un metodo di abbreviazione. Ad esempio, in luogo di «16´16´16» possiamo scrivere, in base alla definizione, «16³». Ma facciamo soltanto questo?

Immaginiamo che le cose stiano così: finora abbiamo imparato ad eseguire moltiplicazioni di vario genere, ci siamo esercitati con numerosi esempi. Con questa regola, attiro la vostra attenzione su questo caso particolare: vi è una classe di moltiplicazioni caratterizzata dall’eguaglianza dei fattori. Questa circostanza è interessante e merita di essere indicata con un nome. Parliamo perciò di un «numero elevato ad una certa potenza»; e in questo modo introduciamo un «nuovo concetto» avviandoci ad elaborare una nuova specie di calcolo.

Finora, probabilmente, ci eravamo già imbattuti in moltiplicazioni i cui fattori erano eguali - ma ad esse non avevamo fatto caso.

Ora abbiamo considerato la nozione di prodotto secondo un nuovo aspetto, abbiamo operato una nuova classificazione, distinguendo tra i prodotti i cui fattori sono eguali e i prodotti i cui fattori non sono eguali. Ed abbiamo portato alla luce nuove connessioni. Ad esempio: qui si richiede che si contino i fattori. Attraverso la definizione mostriamo la connessione «tra la tecnica dell’enumerare i fattori e la tecnica del moltiplicare» (II, 47).

Perciò quando parliamo di «invenzione matematica», o addirittura di «creatività» del fare matematico, con queste frasi vogliamo sostenere qualcosa che sta all’opposto di ciò che esse sembrano suggerire. Può darsi infatti che nella nostra testa ciò che è un fatto tecnico si contrapponga a ciò che è invece un momento di elaborazione concettuale. Ed in fondo, se ci venisse richiesto che cosa intendiamo con un «puro e semplice» fatto tecnico, saremo probabilmente propensi ad indicare esemplificativamente una procedura di esecuzione di una moltiplicazione. Certo, vi sono buone ragioni per pensarla così - una moltiplicazione deve alla fine poter essere eseguita «alla cieca», senza pensarci, e meglio che da noi può essere eseguita da una macchina. Perciò, in generale, un calcolo è un fatto tecnico.

Ma un calcolo viene appunto inventato, non c’è già. E se calcolare significa istituire calcoli, allora dobbiamo sostenere che in nessun modo è lecito divaricare il momento del pensiero matematico da quello della tecnica matematica.

Il pensiero matematico non solo si realizza nel simbolismo, ma poggia in esso. Il simbolismo è attraversato dal pensiero.

9.

Il semplice esempio sul quale ci siamo soffermati indicava in che modo dobbiamo modificare le nostre opinioni di una volta. Poiché non si tratta di mettere in questione la caratterizzazione di principio della’ matematica, ma solo il modo in cui deve essere intesa, tutto il problema può ridursi ad una riconsiderazione di ciò che effettivamente fanno le regole di sostituzione.

Se attraverso le definizioni introduciamo nuovi concetti, passando a nuovi calcoli, non diremo più che esse sono espedienti inessenziali: attraverso questi espedienti, infatti, viene modificata la struttura del simbolismo che diventa ora portatore di nozioni, classificazioni e connessioni che nel simbolismo precedente non erano affatto poste.

Tra i vari interrogativi che possono essere sollevati a questo punto, ve ne è uno che ha un’immediata risonanza di ordine generale. In che modo va inteso il rapporto tra i calcoli, ed in primo luogo il rapporto che sussiste tra il vecchio calcolo ed il nuovo che è stato istituito sul fondamento di quello?

Ritorniamo sull’esempio del passaggio, mediante regole, dal sistema di notazione dei numeri mediante tratti al sistema di notazione decimale.

Il problema del rapporto tra i calcoli si presenta allora in questo modo. Osserveremo anzitutto che qualunque segno numerico nella notazione decimale può essere «ridotto» ad un segno nella notazione mediante tratti. Ma è altrettanto ovvio osservare che questa possibilità è soltanto una possibilità teorica. Di fatto vi è un punto al di là del quale essa cessa di essere effettiva. Così l’uso del metodo notazionale decimale consente di effettuare calcoli che usando l’altro metodo sarebbero di fatto ineffettuabili.

Ora, quando parliamo di un rapporto di fondazione tra i calcoli, quando diciamo che un certo calcolo è fondato su un altro, intendiamo riferirci ad un rapporto di dipendenza inteso nel senso della possibilità di operare una «riduzione». E se vi è un punto al di là del quale questa riduzione cessa di essere effettiva, perché non sostenere che, in questo punto, il nuovo calcolo cessa di dipendere dal vecchio, di essere in esso fondato?

«All’inizio le prove lunghe procedono sempre di pari passo con quelle corte e le accompagnano, quasi ne fossero le tutrici. Infine però non possono più seguire le prove corte, e queste mostrano la loro indipendenza» (II, 45).

«Qui mi sembra che il pericolo consista nel considerare il procedimento abbreviato come una pallida ombra del procedimento non abbreviato» (II, 19).

«Si assume che le definizioni servano soltanto ad abbreviare l’espressione per la comodità di chi esegue il calcolo; invece sono una parte del calcolo» (II, 2).

«Un procedimento abbreviato mi insegna che cosa deve risultare da un procedimento non abbreviato (e non viceversa)» (II, 18).

Accenniamo, cioè, ad un discorso che tende a sottolineare l’autonomia reciproca dei calcoli ed a rendere problematico in che senso si possa parlare di un rapporto di fondazione tra essi. Sulla linea di sviluppo di questo discorso vi è la negazione che dal riconoscimento del sussistere di certi rapporti tra le tecniche calcolistiche sia lecito senz’altro sostenere che questi rapporti possano e debbano essere fissati una volta per tutte secondo un’unica forma di stratificazione sistematica.

Di fronte a questa idea facciamo valere con argomenti di vario genere la possibilità di una molteplicità interamente aperta di modi di organizzazione dei rapporti tra i calcoli; avanziamo dubbi sul senso che ha il problema di un «confronto» tra i calcoli, del controllo di un calcolo mediante un altro (II, 20), ed arriviamo infine a sottolineare l’inscindibilità del nesso tra un calcolo e il suo risultato, tra ciò che viene provato ed il modo in cui lo si prova.

È interessante notare a questo proposito che Wittgenstein stesso rammenta (I, 82) la frase del Tractatus secondo la quale «in matematica processo e risultato sono equivalenti» suggerendo che essa può in fondo essere utilizzata in un senso interamente nuovo: non più per indicare l’indifferenza del processo rispetto al risultato, ma all’opposto per indicare che noi «includiamo il risultato della trasformazione nel modo e nella maniera della trasformazione» (I, 84). Il numero a cui conduce un calcolo «è il termine del processo (fa ancora parte del processo)» (I, 84). E le proprietà dei numeri non sussistono al di fuori del calcolo e di una determinata tecnica di calcolo (II, 58).

Di fronte all’obiezione secondo la quale la possibilità di provare in modi diversi, secondo diverse tecniche di prova, una stessa proposizione mostrerebbe l’indipendenza di questa dal modo della sua acquisizione, affermiamo senz’altro: una proposizione non può avere più di una prova. Questo sembra essere privo di senso: eppure «noi diciamo proprio così» (II, 58).

Le prove effettuate nel sistema notazionale mediante tratti non rendono «costrittive» le prove effettuate nel sistema decimale: «E tuttavia, se non avessimo queste, potremmo usare quelle, per provare la stessa cosa. La stessa cosa? Che cosa è la stessa cosa? Dunque la prova con i trattini mi convincerà della stessa cosa, anche se non nello stesso modo. E se io dicessi: il luogo in cui una prova ci conduce non può essere determinato indipendentemente da questa prova?» (II, 57).

Naturalmente più che negare letteralmente che una stessa proposizione possa essere dimostrata in modi diversi, si tratta di affermare che «ogni prova, anche di una proposizione già provata, è un contributo alla matematica» (II, 60); e forziamo il discorso fino al punto di sostenere che una proposizione non può avere più di una prova perché va respinta fino in fondo la possibilità che, seguendo questa via, venga riproposta, in un modo o nell’altro, l’inessenzialità del «processo» di fronte al «risultato».

Se nella ripetizione di un calcolo ottenessimo risultati di volta in volta diversi cercheremmo certamente di renderci ragione di ciò in circostanze esterne al calcolo (e ciò mostra già che noi includiamo «il risultato della trasformazione nel modo e nella maniera della trasformazione» (I, 86)). Ma allora, se al termine di calcoli di specie diversa ottenessimo uno stesso risultato, questa identità non può essere spiegata facendo riferimento ai calcoli, ma ad «altri contesti» (I, 62) - presumibilmente, al contesto dell’applicazione.

10.

Fin qui non abbiamo fatto altro che illustrare l’eterogeneità della matematica (II, 48).

Abbiamo voluto dire che «la matematica è un miscuglio variopinto di tecniche di prova» (Il, 46). Ma non certo che la matematica è un guazzabuglio di «pure e semplici» tecniche di manipolazione dei simboli nel quale non è nemmeno il caso di tentare di mettere un po’ di ordine!

Illustrare l’eterogeneità della matematica significa elaborare l’idea secondo cui la matematica si muove tra le regole del linguaggio sino al punto di dare pieno risalto al fatto che l’operare matematico è un operare sintetico, e addirittura: sintetico a priori.

Sintetico, perché nella costruzione dei calcoli, nell’invenzione che in essa si realizza, abbiamo a che fare con un’elaborazione ed un incremento concettuale effettivi; ma anche a priori perché abbiamo a che fare appunto con le regole del linguaggio.

A questa espressione, tuttavia, non intendiamo dare un rilievo interpretativo tale da istituire, attraverso di essa, un richiamo immediato al problema kantiano. Al suo uso sarebbe senz’altro opportuno rinunciare se esso fosse inteso come rivolto a stabilire un nesso che in realtà non può che essere molto superficiale.

Ci basti sottolineare - quanto alle differenze - questo punto. Non solo Kant non ha bisogno, nella posizione del carattere sintetico a priori della matematica, di teorizzare una concezione della matematica simile a questa; ma soprattutto è diverso il contesto nel quale quella determinazione viene effettuata. L’obiettivo principale di Kant non era certamente quello di sottolineare la produttività del pensiero matematico, che egli peraltro contrappone alla improduttività della logica. Si trattava invece, nel presupposto del sussistere di una struttura stabile dell’esperienza, quindi dileggi o regole che debbono incondizionatamente valere in essa, di annoverare tra esse le proposizioni matematiche. Dire che queste sono «sintetiche a priori» significa essenzialmente, per Kant, affermare che la matematica «si muove» tra le condizioni di possibilità dell’esperienza. E da questo punto di vista, più rilevante del dettaglio argomentativo con il quale Kant si ingegna a mostrare il carattere non analitico (nel suo senso) delle proposizioni matematiche, è il tentativo di connettere la nozione di numero a quella di successione, e la nozione di successione a quella di successione temporale. Si assume dunque in primo luogo che alla base della matematica vi sia la nozione di numero; la connessione che poi viene istituita tra numero e tempo ha come conseguenza di riferire la matematica intera nell’ambito delle condizioni di possibilità dell’esperienza, a cui la temporalità stessa appunto appartiene, indicando anche la via attraverso cui si dovrebbe giungere ad acquisire una giustificazione assoluta sia della validità transempirica delle proposizioni matematiche, sia della loro applicabilità al mondo dell’esperienza.

Ma l’affermazione dell’eterogeneità della matematica ha anzitutto un significato polemico. Di fronte al programma di dimostrare che la matematica è logica, e quindi di «fondare» la matematica nella logica, attribuendo così ad un calcolo una posizione privilegiata tra i calcoli, di fronte -in altre parole - all’idea di un sistema di organizzazione dei calcoli garantito nella sua struttura e nella sua forma di stratificazione dalla «natura profonda» della matematica, si contrappone l’idea urtante del «miscuglio variopinto di tecniche di prova».

All’omogeneità contrapponiamo l’eterogeneità. E così vogliamo mostrare nello stesso tempo che la matematica non è logica, se affermare che essa lo è ha il senso che gli viene attribuito dal matematico logicista.

«Che cosa vuol dimostrare uno che voglia far vedere che la matematica non è logica? Vuol certamente dire qualcosa del genere; non c e dubbio che se li avvolgiamo in una quantità sufficiente di carta, tavoli, sedie, sbarre, ecc., alla fine ci sembreranno sferici» (II, 53).

11.

È molto difficile accettare senza riserve l’opinione abbastanza diffusa secondo la quale la tendenza intuizionista nella filosofia della matematica avrebbe avuto un peso determinante nella svolta filosofica di Wittgenstein dopo il Tractatus. In realtà, all’interno del dibattito sui fondamenti della matematica negli anni Venti, l’intuizionismo fu, sia in termini negativi che positivi, il punto di riferimento essenziale, il suo momento di interno dinamismo.

È dunque abbastanza ovvio che Wittgenstein fosse particolarmente interessato ai numerosi problemi sollevati dalla tematica intuizionista, mentre il punto di vista del gioco esclude senz’altro qualcosa di simile ad un’influenza tale da determinarne l’orizzonte filosofico.

Del resto, anche quando abbiamo utilizzato il termine di «intuizionismo linguistico» per caratterizzare la posizione del Tractatus, non si tendeva fin da allora a stabilire un legame con la tendenza intuizionista nella filosofia della matematica, ma se mai ad operare una contrapposizione.

Qualunque cosa sia l’intuizione per il matematico intuizionista, essa non è in ogni caso intuizione del linguaggio.

Al contrario, per il matematico intuizionista si tratta di impostare un discorso sull’autonomia della matematica che si precisa in primo luogo come autonomia rispetto al linguaggio. La scelta del termine «intuizione» sottolinea anche questo fatto: un «pensiero» è già formulato in una lingua. E benché il parlare dell’«intuizione matematica» come di una speciale facoltà possa essere più o meno oscuro, è invece del tutto chiaro che in questo modo si vuole sottolineare che il linguaggio, ordinario o meno, ha un obiettivo extra-matematico, che l’essenziale, nel fare matematico, avviene a livelli prelinguistici o alinguistici.

In tutt’altro senso si usava il termine di «intuizione» in rapporto al Tractatus.

Già allora dunque, almeno in questo punto, l’orientamento prevalente del discorso non volgeva in questa direzione; e tanto meno ora, quando diciamo che la matematica si muove tra le regole del linguaggio.

Nemmeno si può sperare di trovare un punto di appoggio nelle affermazioni di Wittgenstein che, in un modo o nell’altro, dicono che «la matematica non è logica». Abbiamo già osservato che affermazioni come queste non vanno prese isolatamente, ma nel contesto di una critica del modo di configurare il rapporto tra matematica e logica da parte logicista. Si tratta allora di mostrare - sviluppando spunti consistenti del Tractatus - che l’errore sta in primo luogo nel ritenere che si possa senz’altro ricondurre ogni espressione matematica sotto il genere di «proposizione» (nel senso in cui normalmente la intendiamo); e che questo non è, in realtà, che il primo passo che conduce alla fine a celare, operando artificiose manipolazioni, la particolarità dei calcoli, e ad attribuire ad uno di essi una pretesa posizione fondamentale.

Certamente, il discorso intuizionista sull’autonomia della matematica si sviluppa anche nel senso di un’autonomia rispetto alla logica. Ma ciò ha poco o nulla in comune con quanto abbiamo or ora sostenuto. Come sappiamo, si tratta in ultima analisi di rifiutare, in determinati casi, certi modelli di prova, traendo da ciò le conseguenze necessarie.

L’interesse di Wittgenstein per questa posizione è fuori di dubbio. E già importante che sia possibile il rifiuto di una prova - e non solo nei giochi infantili da cui abbiamo preso le mosse. Così come è importante, per Wittgenstein, l’intero fascio di problemi che questo rifiuto e le sue ragioni comportano. La presenza della tematica intuizionista, e più in generale, del problema del finitismo, si risente dappertutto nelle Osservazioni sui fondamenti della matematica.

Ma questa tematica è inserita in una cornice filosofica ben diversa da quella espressa dalle posizioni intuizioniste.

Prendiamo l’esempio del «terzo escluso». L’errore del «logico classico», secondo Wittgenstein, sta soltanto in questo: nel fatto di non riconoscere che quando abbiamo introdotto nozioni che implicano totalità attualmente infinite, il gioco è stato effettivamente esteso, si propone qualcosa di effettivamente nuovo, ed allora è lecito pensare che le nostre vecchie regole siano diventate almeno problematiche. Può accadere che l’immagine di un’alternativa, così come viene proposta dal terzo escluso, diventi - in questo caso - vaga e malsicura, che essa cominci a «tremolare» (IV, 10).

È chiaro che non si tratta di mettere in questione la difficoltà rappresentativa, psicologica, dell’infinito «attuale». Una nozione come questa la si potrebbe insegnare anche ai bambini, che la accetterebbero senza difficoltà come accetterebbero che «la terra è un piano infinito; o che dio ha creato un numero infinito di stelle» (IV, 14). Si tratta soltanto della novità del gioco. Abbiamo un gioco e le sue regole. Ora proponiamo di ampliare il gioco in questo modo. Il problema è allora: possiamo giocare il gioco così ampliato con le vecchie regole?

Per l’intuizionista la risposta è precisa: queste leggi logiche, in questo caso, non valgono più. Ed altrettanto precisa è la risposta del «logico classico»: la logica ha una validità assoluta e incondizionata, si applica a questo caso come ad ogni altro.

Secondo Wittgenstein entrambe le posizioni sono erronee:

«Quando un nostro amico ci riempie la testa con il principio del terzo escluso a cui non si può sfuggire allora è chiaro che nella sua domanda c’è qualcosa che non va» (IV, 10). Ma anche: «La considerazione secondo cui una legge logica, poiché vale per una sfera della matematica, non necessariamente vale per un’altra, non è affatto a posto nella matematica, ed è del tutto contro la sua natura. Benché molti autori la ritengano particolarmente sottile e spregiudicata» [2].

Di fatto, nell’ampliamento del gioco, qualcosa resta indeterminato. Qui vi è lo spazio per una decisione. Perché non dovremmo poter estendere il gioco in questo modo? Oppure: perché non dovremmo poter trovare un senso nuovo per le vecchie regole?

La posizione di Wittgenstein assume un risalto, se possibile, ancora più chiaro, in rapporto al problema della connessione tra esistenza matematica e costruttività.

Abbiamo insistito in precedenza su questo punto: non dobbiamo separare la prova dal suo risultato. Dobbiamo sempre dire: abbiamo provato questo e lo abbiamo provato così. Il modo della prova è essenziale per determinare che cosa abbiamo provato.

Ma allora anche l’intuizionista effettua questa separazione nello stesso momento in cui avanza la pretesa di presentare la propria nozione di esistenza come la vera nozione di esistenza matematica. Per l’intuizionista vi è un’unica nozione di esistenza matematica: per Wittgenstein ve ne possono essere ben due.

«Ogni dimostrazione di esistenza deve contenere una costruzione di ciò la cui esistenza essa dimostra». Si può dire soltanto: ‘Io chiamo dimostrazione di esistenza solo una dimostrazione che contenga una tale costruzione’. L’errore sta nella pretesa di possedere un chiaro concetto di esistenza. Si crede di poter dimostrare qualcosa, l’esistenza, in modo tale da essere convinti di essa indipendentemente dalla dimostrazione... In realtà l’esistenza è ciò che si dimostra con ciò che si chiama dimostrazione di esistenza. Trattando di ciò, gli intuizionisti e gli altri dicono: ‘Questo stato di cose, l’esistenza, lo si può dimostrare solo così, e non così’. E non vedono che essi hanno con ciò definito semplicemente ciò che essi chiamano esistenza» [3].

Anche nei confronti del matematico intuizionista può dunque essere ripetuto ciò che avevano detto a suo tempo nei confronti del matematico logicista. Il matematico intuizionista non può fare altro che presentare le proprie regole: «D’ora in poi inferirò in questo modo e pertanto esso dovrà considerarsi corretto» (I, 20). Anche nel caso della filosofia intuizionista della matematica la sussistenza di una discriminazione tra senso e nonsenso come discriminazione assoluta ed oggettiva rappresenta un ovvio presupposto. Mentre: «La proposizione matematica deve proprio mostrare che cosa abbia senso dire. La prova costruisce una proposizione: ma ciò che importa è il modo in cui la costruisce. Qualche volta, per esempio, costruisce dapprima un numero; di qui, poi, segue, la proposizione che un numero siffatto esiste. Quando diciamo che la costruzione dovrebbe convincerci della proposizione, questo vuol dire che essa deve indurci ad applicare questa proposizione in questo modo così e così, che deve determinarci a riconoscere questa cosa come sensata, quest’altra come priva di senso» (II, 28).

«Di qui la disputa se una prova di esistenza che non è una costruzione sia una effettiva prova di esistenza. Sorge cioè la questione: comprendo la proposizione ‘Esiste un...’ quando non ho alcuna possibilità di trovare il luogo in cui questa cosa esiste? E a questo proposito ci sono due punti di vista: come proposizione della lingua italiana (per esempio) la comprendo, cioè posso spiegarla... Ma che cosa posso farne? Ebbene, non la stessa cosa che posso fare con una prova costruttiva» (IV, 46).

«Non soltanto la prova di esistenza può lasciare indeterminato il luogo dell’‘esistente’: ma non è affatto necessario prendere in considerazione un luogo del genere. In altre parole: se la proposizione provata suona: ‘esiste un numero tale che...’, allora non deve di necessità avere senso il chiedere ‘e qual è questo numero?’ o il dire ‘e questo numero è...’» (IV, 26).

12.

La ben nota immagine secondo la quale «i problemi matematici dei cosiddetti fondamenti non fondano per noi la matematica più di quanto una roccia dipinta sostenga un castello dipinto» (V, 13); o altre affermazioni estreme che sembrano condurre ad un’esplicita negazione della sussistenza del problema, in una forma che di primo acchito non solo stentiamo ad accettare, ma addirittura a comprendere, diventano immediatamente intelligibili se vengono intese come un attacco condotto da Wittgenstein con estrema asprezza contro una determinata idea del compito proposto sotto il titolo di «fondazione della matematica»: secondo Wittgenstein, in coerenza con l’intera posizione filosofica generale che abbiamo delineata, «fondare la matematica» non può in ogni caso volere dire acquisire per essa un fondamento assoluto e certo - non può voler dire, appunto, mostrare come le radici della matematica affondino, per usare un’immagine di Frege, su una «roccia eterna».

Di qui la critica verso il logicismo; ma di qui anche quella nei confronti dell’«assolutismo» intuizionista: in esso questa idea è tanto presente ed operante che sembra essere l’unico elemento a cui ci si possa appigliare per rendersi ragione del radicalismo intuizionista per una nuova fondazione, per un completo rinnovamento che comincia con il fare tabula rasa delle conquiste «paradisiache» della matematica moderna e non esita a mettere in dubbio posizioni metodiche solidamente assicurate.

In questo attacco, e secondo questa stessa prospettiva, deve alla fine essere coinvolta anche l’idea della fondazione che sta alla base del programma hilbertiano della «teoria della dimostrazione».

Nel presentare questo programma, nel 1922, Hilbert traccia in breve questi nessi: il problema dei fondamenti della matematica fa tutt’uno con quello della sua certezza, con lo scopo di dare «una fondazione sicura alla matematica», in modo da restituire ad essa «la sua antica fama di verità incontestabile» che sembra compromessa dalla scoperta delle contraddizioni nella teoria degli insiemi.

All’organizzazione teoretica delle proposizioni matematiche in un sistema di assiomi, deve seguire la prova dell’inderivabilità in esso di una contraddizione. In assenza di questa prova si può sempre dubitare che una contraddizione possa ad un certo punto presentarsi. Mentre «se questa dimostrazione ci riesce, avremo accertato con ciò che gli enunciati matematici sono effettivamente verità incontestabili e definitive - una conoscenza che è della massima importanza per noi anche per via del suo carattere filosofico generale» [4].

È importante infatti, in generale, mostrare che tra tutte le certezze presunte, ve ne sono alcune che lo sono in modo indubitabile.

Questo sfondo nel quale il problema viene proposto, chiarisce subito l’angolatura dalla quale Wittgenstein lo affronta. Esemplare diventa non tanto il programma stesso nelle sue specificazioni quanto l’atteggiamento che sta ai margini di quel programma.

L’attacco di Wittgenstein è, per così dire, un attacco a ciò che vi è di cartesiano nella posizione di Hilbert. Ed ha lo scopo primario di mostrare che l’attribuzione a questo problema di una valenza filosofica attraverso cui esso si prolunga in un discorso sulla certezza può essere motivata soltanto da un pregiudizio.

Chiariamo allora subito il punto principale:

«Una cosa è una tecnica matematica che consente di evitare la contraddizione, ed un’altra cosa è filosofare in generale contro la contraddizione in matematica» (III, 55).

Con ciò separiamo fin dall’inizio, e molto nettamente, ciò che in Hilbert è di fatto l’ invenzione di un «nuovo pezzo di matematica» (V, 9) da ciò che invece rinvia soltanto ad un atteggiamento nei confronti della contraddizione. In nessun caso si tratta di mostrare che la posizione di questo programma e ciò che può essere eventualmente acquisito nel suo concreto sviluppo sia qualcosa di irrilevante: «Come potrebbe essere così?».Lo scopo è invece quello di «cambiare l’atteggiamento nei confronti della contraddizione e della prova di non contraddittorietà» (II, 82).

Per questo motivo il riferimento a Hilbert tende a diventare essenzialmente un pretesto, e per mostrare quali siano le conseguenze della posizione generale di Wittgenstein in rapporto a questo problema basterà accennare alla messa in questione della sua posizione iniziale attraverso un’elementare utilizzazione dell’analogia con il gioco. Se ciò che Hilbert propriamente fa è l’invenzione di un nuovo pezzo di matematica, è importante anzitutto cercare di rendersi conto del significato che può avere parlare di «metamatematica» in rapporto alla «teoria della dimostrazione». In Hilbert la proposta metodica consiste in un’estensione a questo problema della posizione delineata in rapporto alla «teoria elementare dei numeri»: oggetto delle nostre considerazioni «contenutistiche» sono ora gli assiomi nella loro struttura figurale, ed il problema è quello di mostrare in modo diretto che da tali strutture è inderivabile una certa figura assunta come «equivalente formale» della contraddizione. Il linguaggio della teoria della dimostrazione è perciò un linguaggio che parla di un linguaggio - il piano su cui ci muoviamo non è «matematico», ma «metamatematico»Per spiegarci potremmo richiamarci appunto alla differenza tra il gioco e la teoria del gioco. Questa illustrazione analogica viene invece utilizzata da Wittgenstein nella direzione opposta.

Nei colloqui con Waismann e Schlick, Wittgenstein argomenta una volta così: immaginiamo di voler dimostrare nella teoria del gioco degli scacchi che in otto mosse mi è possibile raggiungere una data disposizione di pezzi sulla scacchiera. Ora nella teoria del gioco mi servirò di un simbolismo, e nella dimostrazione si fa in questo simbolismo ciò che si potrebbe fare senz’altro con i pezzi sulla scacchiera: «Ho eseguito le mosse appunto simbolicamente. Ciò che manca è in realtà solo il movimento effettivo; e siamo d’accordo sul fatto che lo spostamento delle figure di legno sulla scacchiera è qualcosa di inessenziale» [5].

Naturalmente, l’osservazione funziona solo nei limiti dell’esempio addotto. Potrebbe darsi che nella teoria del gioco si possa dimostrare qualcosa che non si può invece mostrare muovendo i pezzi sulla scacchiera. Ma qui si tratta di vedere se un’osservazione come questa sia o meno nella direzione giusta, se cioè sia giusto cominciare con l’ affermare che «ciò che si chiama ’teoria del gioco degli scacchi’ non è una teoria che descrive qualcosa, ma una sorta di geometria. Essa è naturalmente ancora un calcolo, e non una teoria» [6]

Se si può essere d’accordo su questa linea di discorso, allora si dovrà ammettere anche che nel passare dalla «matematica» alla «metamatematica» non si fa altro che passare da certi calcoli ad altri calcoli, che introdurre la «metamatematica» è introdurre un calcolo, ed eventualmente un «nuovo» calcolo (e non solo una traduzione del vecchio calcolo in un simbolismo diverso). In questo senso possiamo dire che la «metamatematica» è semplicemente «matematica»: Hilbert non fa altro che «istituire le regole di un determinato calcolo come regole della metamatematica» [7]. L’errore nell’impostazione del problema sta allora anzitutto nel ritenere che un calcolo, che è un «pezzo di matematica», possa presentare «chiarimenti di principio sulla matematica» [8].

Del resto l’analogia con il gioco può essere utilizzata anche nell’altra direzione, in rapporto al problema della contraddizione. Non ci è affatto chiaro, anzitutto, che cosa si possa intendere con «contraddizione» in un gioco e come si ponga, in rapporto al gioco, il dubbio sulla sua possibilità.

Potremmo forse pensare ad una situazione di questo genere: ad un certo punto del gioco, in una certa posizione dei pezzi sulla scacchiera, accade questo: dobbiamo muovere un pezzo secondo una certa regola; e non lo possiamo muovere secondo un’altra regola.

Il gioco si blocca. Non sappiamo più che cosa fare. Possiamo smettere di giocare, oppure giocare in un modo qualsiasi, a casaccio. Siamo, per così dire, abbandonati dalle regole. Nulla è più possibile, oppure tutto è possibile.

Ma potremmo anche decidere di modificare le vecchie regole, di inventare regole nuove. Supponiamo ora che in questo gioco non si sia mai presentata una situazione di contrasto tra le regole. Per questo noi crediamo si tratti di un gioco «vero e proprio» e ci affidiamo senz’altro alle sue regole. Il dubbio è tuttavia sempre possibile: nessuno ha mai dimostrato che il gioco sia veramente in ordine, in ogni caso può sempre esserci una contraddizione nascosta[9].

Peraltro, se un giocatore ci proponesse questo problema prima di accingerci a giocare, probabilmente reagiremmo osservando: intanto giochiamo. All’apparire della contraddizione decideremo qualcosa.

Ma che cosa si pretende di mostrare con osservazioni come queste? Non è forse chiaro che qui l’analogia ci tradisce suggerendo argomenti che falliscono interamente il problema effettivo proposto?

In esso non era certo in questione la possibilità di esercitare un calcolo che non sia garantito in questo modo. Ciò del resto è sempre accaduto nell’esercizio della nostra aritmetica.

Obiettiamo dunque che basta questo inizio per mettere allo scoperto che qui si confonde la «sicurezza» con la quale noi di fatto procediamo nel calcolo, e la «sicurezza» che deve spettare al calcolo stesso: la sua sicurezza «ideale» (V, 28).

In realtà per Wittgenstein non si tratta certo di contrappone l’uno all’altro piani di discorso che in effetti sono incommensurabili. Non si tratta, cioè, di contrapporre alla richiesta di una dimostrazione di non contraddittorietà dell’aritmetica il fatto che questa comunque ha reso finora «ottimi servigi» (V, 28). Altrimenti la tesi di Wittgenstein sarebbe proprio che il programma di Hilbert rappresenta qualcosa di «irrilevante» - una tesi che si spiegherebbe solo nel quadro di un semplicistico ed ottuso pragmatismo.

Quelle osservazioni puntano piuttosto alla messa in questione della contraddizione come un problema cruciale accentuando il riferimento al piano linguistico e indebolendo, per così dire, il suo peso ontologico.

Per Wittgenstein non vi è dubbio che la non contraddittorietà di un calcolo rappresenti un problema matematico effettivo, che vi sono calcoli impiegati per scopi che «rendono indesiderata una contraddizione». Ma il punto di vista del gioco insegna anche che fra i giochi ve ne possono essere alcuni nei quali la contraddizione rappresenta «una parte assolutamente rispettabile» (II, 80).

13. L’atteggiamento nei confronti della contraddizione che rappresenta l’obiettivo polemico di Wittgenstein aveva trovato proprio nel Tractatus una sua formulazione esemplare. In esso si mostrava in che modo la teorizzazione dell’idea di un linguaggio interamente attraversato dall’ordine della logica fosse connessa ad un determinato atteggiamento nei confronti della realtà. Per questo, tanto più mordace è la polemica su questo punto, tanto più si assumono toni di scherzo che raggiungono l’asprezza del sarcasmo, quanto più oggetto del sarcasmo è anzitutto Wittgenstein stesso, il Wittgenstein di una volta. E nello stesso tempo il carattere di pretesto del riferimento alla «prova di non contraddittorietà» si accentua sino a diventare non più che un appiglio letterario nel quale si hanno ormai di mira tutt’altri contesti.

Che cosa è ora la contraddizione si illustra attraverso metafore come queste:

Nel calcolo è entrata la confusione. Non riusciamo più a raccapezzarci. «Questo dunque è il male». «Una malattia diffusa per tutto quanto il corpo». Una malattia segreta. Un abisso che forse non vediamo. Ad ogni passo corriamo il rischio di cadere in un pantano. Una nuova forma di pazzia.

E così diventa un immagine anche la «prova di non contraddittorietà»: «Che cosa richiedono mai quando esigono una prova di non contraddittorietà perché altrimenti ad ogni passo correrebbero il rischio di cadere nel pantano?- Ebbene essi esigono un ordine, Ma non c’era nessun ordine, prima? - Ebbene esigono un ordine che li rassicuri » (II, 78).

Al «vago timore» che un giorno una cosa qualsiasi possa «in qualche modo, venire interpretata come la costruzione di una contraddizione» (Il, 87), all’«angoscia superstiziosa» di fronte alla contraddizione (I, App. I, 17) come immagine di disorientamento e di perdita si contrappone l’istanza di una realtà per noi «sicura», che possegga dunque un ordine, una struttura stabile e ben nota.

Noi ci accingiamo allora ad una parodia della sicurezza:

«Ebbene esigono che li rassicuri. - Ma sono forse bambini che basta cantargli la ninna nanna?» (II, 78).

«Ma il nostro ideale deve essere proprio la tranquillità (il nostro ideale deve essere che ogni cosa sia avvolta nel cellophane)?» (II, 81).

«E se è vero che vado in cerca di avventure allora non posso andare in cerca di quelle avventure nelle quali questa prova non mi offre più alcuna sicurezza?» (II, 82).

«Perché non potrebbe darsi che volessimo produrre una contraddizione? Che dicessimo - con l’orgoglio di chi ha fatto una scoperta matematica: »Guarda, in questo modo produciamo una contraddizione«? Non può darsi, per esempio, che molta gente abbia tentato di produrre una contraddizione nel dominio della logica e che, finalmente, uno di loro ci sia riuscito?» (II, 81).

È chiaro che dovevamo giungere a questo: dall’idea che il gioco debba essere giocato solo con strade diritte (II, 79) all’idea che il linguaggio sia un labirinto di strade [10]; dall’idea che la contraddizione non sia altro che un ingarbugliarsi di strade all’idea che la contraddizione stessa possa essere una strada. Forse anche quella che passa più vicino alla nostra realtà. Lo strano personaggio che abbiamo evocato or ora e che a tutti i costi tenta di produrre una contraddizione e alla fine ci riesce in mezzo alla soddisfazione generale vuol forse mostrare che «in questo modo tutto è incerto», che «noi viviamo nelle vicinanze della contraddizione» (II, 81) - e ce ne assumiamo la responsabilità.

Una responsabilità che è poi essenzialmente pratica: nella contraddizione dobbiamo fare qualcosa. La contraddizione è una sorta di ammonimento degli dei: «Devi agire, e non riflettere!» (III, 56).

Quanto alla responsabilità, per così dire, teoretica della certezza sembra a Wittgenstein che forse la Possiamo allontanare da noi così come allontaniamo il vecchio mito cartesiano. Di una simile certezza - di una certezza «cartesiana» non abbiamo affatto bisogno. il riferimento diventa esplicito nel momento in cui Wittgenstein si richiama, a modo suo, al dubbio sulla veglia e sul sonno:

«Come sonnambuli, stiamo percorrendo una strada sospesa tra due abissi. - Ma se anche ora diciamo: ’Adesso siamo svegli’ - possiamo essere sicuri che un giorno non ci sveglieremo? (E allora diciamo: dunque abbiamo di nuovo dormito)» (II, 78).

Dovremmo allora andare alla ricerca di un punto in cui sia possibile operare questa discriminazione, un punto interamente illuminato dalla ragione nel quale, come esseri razionali, siamo indubitabilmente desti?

Il fatto è che questo problema ci lascia completamente indifferenti.

Arriviamo alla parodia popolaresca: «Nessun diavoletto ci inganna in questo momento? Bene, se ci inganna non importa. Occhio non vede, cuore non duole» (II, 78).

Del resto, accanto a Cartesio, possiamo anche evocare il nome di Leibniz, e nella stessa direzione, cioè come simbolo di un ideale rispetto al quale opponiamo ora una aperta negazione. Rileggiamo il passo famoso di Leibniz: «Per tornare all’espressione dei pensieri per mezzo di caratteri, sento che le controversie non finirebbero mai e che non si potrebbe mai imporre il silenzio alle sette, se non ci riportassimo dai ragionamenti complicati ai calcoli semplici, dai vocaboli di significato vago e incerto ai caratteri determinati.

Occorre, cioè, far si che ogni paralogismo sia nient’altro che un errore di calcolo, e che ogni sofisma, espresso in questo genere di scrittura, nient’altro sia che un solecismo o barbarismo, da sciogliere facilmente mediante le stesse leggi di questa grammatica filosofica.

Una volta fatto ciò, quando sorgeranno delle controversie non vi sarà maggior bisogno di discussione tra due filosofi di quanto ce ne sia tra due calcolatori. Sarà sufficiente, infatti, che prendano la penna in mano, si siedano a tavolino, e si dicano reciprocamente (chiamato, se loro piace, un amico): ’calcoliamo’» [11].

Di fronte a ciò diciamo semplicemente: «Nessun calcolo può decidere un problema filosofico» [12]. Nel punto focale di questa duplice negazione, la contraddizione può alla fine diventare il tema per un apologia.

Note

[1] Philosophische Grammatik, op. cit., p. 306.

[2] ivi, 458.

[3] ivi, p. 374

[4] D. Hilbert, Neubegründung der Mathematik. Erste Mitteilung, in D. Hilbert, Gesammelte Abhandlungen, Berlin 1970, p. 162.

[5] Wittgenstein und der Wiener Kreis, op. cit.. p. 133.

[6] ivi.

[7] Philosophische Grammatik, op. cit., p. 297.

[8] ivi, p. 296

[9] Wittgenstein und der Wiener Kreis, op. cit, p. 174.

[10] Ricerche filosofiche, ed. it. a cura di M. Trinchero, Torino 1967, p. 109 (oss. 203).

[11] G.W. Leibniz, Scritti di logica, op. cit., p. 237.

[12] Philosophische Grammatik, op. cit., p. 296.

Capitolo V

Copertina