Paolo Spinicci

Il mondo della vita e il problema della certezza
Lezioni su Husserl e Wittgenstein

 Lezione terza

1. La natura e le formule

Le considerazioni che abbiamo precedentemente svolto ci hanno condotto ad una duplice tesi che è opportuno rammentare: da un lato infatti abbiamo messo in luce la tendenza della riflessione galileiana ad interpretare l'obiettività della scienza alla luce dell'istanza platonica della metessi, dall'altro abbiamo invece richiamato l'attenzione sull'importanza che Husserl attribuisce alla prassi di idealizzazione che è implicata dall'idea di natura che la scienza galileiana ci propone - un'idea di natura che è caratterizzata dal suo porsi come un costrutto teorico il cui senso non può essere pienamente compreso se non ripercorrendo quel processo di idealizzazione e di costruzione ipotetica, le cui tappe sono state sommariamente indicate nella prima parte del paragrafo nono della Crisi. Ma se in questa prospettiva il momento della costruzione acquista la centralità che gli compete, diverso è l'esito cui doveva condurre lo sviluppo della scienza galileiana, - uno sviluppo che in questo caso non chiama in causa l'interpretazione filosofica che lo scienziato dà della sua prassi, ma il senso che i risultati che ne derivano tendono di per se stessi ad assumere. Che cosa Husserl intenda può essere detto in breve. La scienza mira alle formule, e cioè alla determinazione funzionale delle relazioni tra le grandezze ottenute come risultato della misurazione; solo da questa coordinazione funzionale è infatti possibile ricavare previsioni:

Riconoscere l'importanza teorica e pratica delle formule è importante, per Husserl, poiché proprio a partire di qui si deve muovere per comprendere il mutamento di senso che doveva colpire la prassi scientifica e l'idea stessa di una conoscenza obiettiva. Le formule sono oggetti matematici, e anche se il senso che le caratterizza può essere effettivamente attinto solo richiamando alla mente il processo della loro costituzione e il loro necessario riferimento al mondo intuitivo, resta comunque vero che è possibile una loro considerazione puramente astratta e formale. Potremmo forse esprimerci così: il cammino che ci conduce alle formule non è necessario per comprendere la formula il cui senso operativo si dispiega solo all'interno della teoria cui appartiene. Le formule della fisica debbono essere infine comprese solo per quello che sono - formule ben formate di una teoria data.

Le tappe in cui questo necessario cammino si articola sono molteplici; Husserl, tuttavia, si sofferma solo su due differenti aspetti che ci riconducono dal terreno delle scienze naturali all'ambito della matematica: il momento della formalizzazione ed il momento, ad essa connesso, del calcolo. Il primo tema ci riconduce ad alcune considerazioni di carattere generale sulla storia della matematica: l'introduzione in età rinascimentale delle designazioni algebriche, la nascita della geometria analitica con Cartesio, l'aritmetizzazione dell'analisi numerica, e - infine - quella dottrina delle molteplicità definite in cui Husserl vede l'esito cui il pensiero matematico a lui contemporaneo è giunto.

Non è possibile qui soffermarsi sul significato che deve essere attribuito a questi brevi cenni di Husserl; del resto, ai fini delle nostre considerazioni è più che sufficiente richiamare brevemente uno degli snodi teorici cui queste pagine alludono: il sorgere della geometria analitica. Ci ricordiamo tutti dell'equazione della retta:

E ci ricordiamo anche delle ragioni che ci permettono di introdurre una simile formula: se traccio gli assi cartesiani, ogni punto del piano può essere individuato da una coppia di numeri reali. Ora, per individuare una retta sul piano debbo poter indicare per ogni punto che le appartiene la coppia di numeri reali che lo individua - debbo in altri termini costruire una funzione che, posto un qualunque numero reale come suo argomento, determina il valore di un altro numero reale in modo tale da fissare le coordinate di un un punto che alla retta appartenga. Abbiamo cioè una funzione y=f(x) - una funzione che, nel caso della retta, è particolarmente semplice, così come semplice è la comprensione dell'equazione da cui abbiamo preso le mosse.

E tuttavia la semplicità non si lega più ad un rimando alla dimensione intuitiva. Scriviamo l'equazione e comprendiamo come stanno le cose. Se l'equazione è

e se per comodità prendiamo il caso in cui c=0, allora possiamo dire che y = -a/b(x) e cioè che il rapporto tra x e y è costante (-a/b=m).

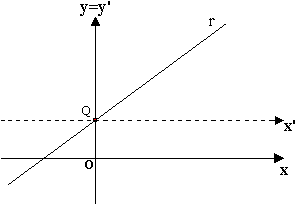
Ora, la costante m è il coefficiente angolare della retta ed in questa espressione ci sembra ancora che si possa vedere qualcosa: guardiamo il grafico che corrisponde alla funzione e ci sembra ancora di poter vedere nell'inclinazione della retta la ragione del rapporto tra le ascisse e le ordinate. E tuttavia anche da questo ricordo spaziale possiamo prendere commiato poiché è possibile esprimersi diversamente: possiamo dire infatti che una retta r è il luogo dei punti del piano per i quali il rapporto tra l'ascissa e la coordinata è eguale a una costante m. O ancora: che è il luogo dei punti individuati su un piano dalle coppie di numeri reali generati dalla funzione y=mx.

La retta, diceva Euclide, è ciò che giace egualmente tra due punti, ed anche se questa definizione esprime già l'intenzione di ricondurre la dimensione intuitiva della forma in un sistema di proposizioni che garantisca l'applicazione dello strumento deduttivo, è evidente che qui il ponte con l'intuizione non è stato ancora rescisso. Tracciamo la retta sul foglio e diciamo che giace in modo eguale, poiché la mano non si piega mai a seguire una diversa direzione, poiché non vi è mai una decisione nuova ed imprevista - e di questo linguaggio immaginoso possiamo avvalerci proprio perché nella definizione euclidea resta ancora l'eco remota di un passato intuitivo.

Forse si converrà che le cose stanno proprio così, che in Euclide vi è ancora il ricordo dello spazio intuitivo che del resto è racchiuso nell'etimo di molte parole geometriche - nella parola "geometria" risuona ancora la presenza della terra, il triangolo isoscele è, etimologicamente, un triangolo che ha le gambe eguali, mentre - assicura Proclo - il triangolo scaleno si chiama così perché zoppica. Forse lo si riconoscerà - ma che conseguenza dobbiamo trarne? Dobbiamo forse lamentarci del nostro presente e rimpiangere l'età di Euclide in cui ancora nomi e concetti risuonavano della nostra concreta esperienza spaziale?

Naturalmente no. Leggere le pagine husserliane come se fossero l'espressione di una nostalgia filosofica per un'epoca passata della storia della scienza vorrebbe dire fraintenderle interamente. Su questo non possono esservi dubbi, per Husserl: la geometria doveva percorrere il cammino dell'analisi e doveva diventare una disciplina puramente formale, e chi legga la Crisi rammentandosi delle considerazioni conclusive dei Prolegomeni per una logica pura che Husserl pubblica nel 1900 come primo volume delle Ricerche logiche non può non scorgere nella terminologia che viene proposta per delineare brevemente lo sviluppo del pensiero geometrico la convinzione husserliana di avere contribuito in modo significativo alla comprensione filosofica di quel necessario cammino. Eppure, alla storia del sapere geometrico si lega un passo falso nella storia del pensiero - il passo falso di una filosofia che sorge insieme allo sforzo di assiomatizzazione dell'universo matematico, giustificandolo ora in chiave platonica, ora in chiave convenzionalistica. Due vie differenti che hanno tuttavia un punto in comune: per il filosofo platonico o per il teorico delle convenzioni, la geometria ha negli assiomi il suo cominciamento assoluto, e tutto ciò che la precede può essere semplicemente dimenticato. O frainteso: la logica delle figure intuitive e dei procedimenti operativi deve essere ricondotta ad un'applicazione inconsapevole di assunzioni implicite, - deve, in altri termini, essere ricondotta alla dimensione assiomatica. Quanto poi alla domanda sul senso e sulla legittimità degli assiomi, il filosofo platonico ed il teorico del convenzionalismo si trovano d'accordo nel negare la legittimità di un simile interrogativo: al di là degli assiomi non si può andare, poiché l'inizio della geometria è un inizio assoluto. Dall'intuizione della figura non si può imparare nulla, poiché possiamo cogliervi soltanto ciò che in virtù del sapere matematico vi abbiamo già proiettato: se la geometria nasce come un sistema proposizionale di natura deduttiva, diviene insensato domandarsi che cosa vi sia prima delle assunzioni da cui la deduzione può prendere le mosse.

Di qui il paradosso su cui Husserl ci invita a riflettere. La storia della geometria - il suo sviluppo da teoria intuitiva delle forme a pura molteplicità matematica definita assiomaticamente - doveva di fatto giustificare le pretese di una filosofia secondo la quale la geometria non ha storia, poiché l'ideale non è il risultato di una prassi, ma un dato obiettivo, un oggetto ideale circoscritto da una definizione o da una convenzione stipulata linguisticamente.

Del resto, in questa direzione doveva condurre anche un altro sviluppo implicito nel pensiero matematico - la sua tendenza a tradurre le operazioni concettuali in procedimenti calcolistici. Anche in questo caso sarebbe senz'altro sbagliato cogliere in questa piega del pensiero matematico un procedimento illegittimo. Tutt'altro: la forma calcolistica appartiene necessariamente al pensiero matematico e l'ideale di Lambert secondo cui si deve ricondurre la teoria delle cose alla teoria dei segni è uno dei cardini teorici del pensiero husserliano sin dal tempo della Filosofia dell'aritmetica. Ma ancora una volta, ciò che matematicamente è legittimo si lega ad una conclusione impropria: la conclusione secondo la quale ciò che conta sono infine soltanto le formule e le regole operative che ci consentono di calcolare. E ciò è quanto dire che il costituirsi della matematica come arte calcolistica facilita il venir meno del nesso che lega la geometria e l'aritmetica al terreno pre-teoretico da cui pure sorgono:

Manca, lo ripetiamo, se ci disponiamo in una prospettiva filosofica. Ciò su cui Husserl intende attirare l'attenzione è riconducibile infatti a questa tesi di fondo: la storia della geometria doveva rendere plausibile una riflessione filosofica che fa di ciò che è ideale non già il risultato di una prassi condivisa ed intuitivamente fondata, ma un oggetto di cui non si deve rendere conto, poiché ha già nella sua lontananza dalla sfera di ciò che è sensibile il contrassegno ontologico della sua certezza. Ad una concezione filosofica che sottolinea la genesi ideale dei concetti geometrici da una prassi teorica che si radica nel mondo della vita doveva sostituirsi così la tesi della discontinuità tra ragione e vita: per il rinnovato platonismo dell'età moderna le verità geometriche dovevano porsi come un oggetto chiuso in se stesso, come un insieme di proposizioni che solo accidentalmente mostrano un volto intuibile.

Di qui il riproporsi del modello della metessi da cui abbiamo preso le mosse. Una volta rescisso il nesso tra la geometria come logica intuitiva delle figure e la geometria come sistema di proposizioni sintatticamente connesse doveva divenire problematico il come dell'applicazione della geometria al mondo in cui viviamo. Per questo problema la filosofia moderna doveva trovare una risposta che, per Husserl, è solo un modo per tacitare la domanda: il filosofo dell'età moderna poteva rendere conto dell'applicazione della geometria e del metodo scientifico al mondo della vita solo cedendo alla convinzione secondo la quale il mondo è davvero scritto in termini matematici, ed i fenomeni sensibili sono davvero soltanto fenomeni - ombre di un mondo trascendente, i cui contorni possono essere tracciati soltanto dall'idealità del numero. Il mondo, questo mondo in cui viviamo, doveva apparire così come l'ombra di un mondo vero in sé - il mondo matematico scoperto dalla riflessione scientifica:

Dimenticato il processo di idealizzazione della natura, scordata la prassi intersoggettiva della ricerca scientifica e messo da parte il processo apertamente infinito della verificazione, il mondo matematico scoperto dalla scienza assume le forme di un vero essere, - di un mondo obiettivo che sta dietro ai fenomeni e li fonda nella loro apparente realtà. L'abito ideale che la scienza confeziona copre il mondo della vita e lo sostituisce agli occhi degli scienziati e degli uomini colti:

E ciò è quanto dire che il venir meno della dimensione costruttiva della scienza si traduce in un'obiettivazione della verità scientifica - in un obiettivismo che rende di fatto problematico il rapporto tra l'essere vero della scienza e il mondo della vita - "quell'unico mondo reale che si dà realmente nella percezione" (ivi, p. 77).

INDICE  

§ precedente

inizio pagina

§ successivo