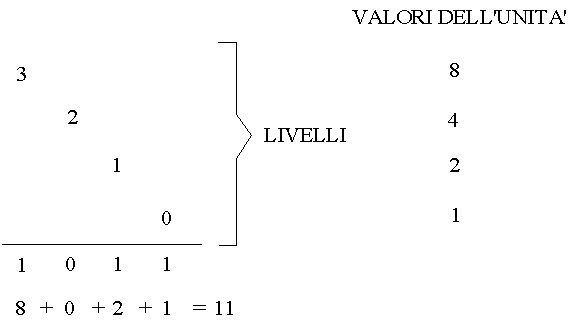
|
Idee per un’epistemologia della ripetizione |
|
Giovanni Piana
|
15
- I numeri distributivi e l’idea di una base
- La domanda «Quanti per volta?»
- Ai metodi additivi manca l’idea di grande unità ottenuta ricorsivamente
- Intreccio tra concetto e rappresentazione
- Grande unità, ricorsione e notazione posizionale.
Questo intreccio diventa chiaramente visibile nella questione della base. Si tratta infatti di un’elaborazione della tecnica elementare del conteggio che da un lato interviene a livello concettuale e dall’altro mette in questione il piano simbolico notazionale. |1|
Ripensiamo al filo conduttore linguistico che ci ha permesso di parlare di numeri cardinali, ordinali e iterativi. In quella nostra discussione avevamo omesso un altro caso interessante di forma espressiva relativa ai numeri registrata dalla grammatica corrente. Si tratta di espressioni del tipo «a due a due», «a tre a tre» ecc., ovvero dei numerali detti correntemente «distributivi». In latino, oltre Quot? Quotus? Quoties?, il «quanti» assume anche la forma del Quoteni? ovvero del «Quanti per volta?». Le risposte richiederanno poi l’impiego di parole numeriche particolari come singuli, bini, terni, quaterni, ecc. |2|
Naturalmente è qui implicato il problema di un’operazione di raggruppamento, ma non nel senso da implicare una molteplicità data, che viene in qualche modo concretamente divisa, ad esempio in cinque parti. Il conteggio con cui si risponde al «Quanti per volta?» può ovviamente iniziare anche se non la molteplicità a cui ci si riferisce non è attualmente presente nella sua totalità. |3|
Nello stesso tempo il numero in quanto numero-di-oggetti ritorna all’interno del nostro problema. |4|
Se, data una certa molteplicità, debbo prendere da essa quattro elementi per volta, conterò anzitutto fino a quattro (possiamo in proposito pensare anche anche un modo primitivo di «conteggio»), ed opererò in questo modo un primo raggruppamento, e poi ancora fino a quattro, ed opererò un secondo raggruppamento, e così via. Perciò svolgono qui una parte essenziale anche il numero ordinale e il numero di volte. Il numero di volte riguarda l’operazione del conteggio e il conseguente raggruppamento - e sappiamo già che vi è una connessione di principio tra ordine e iterazione. |5|
Le considerazioni sulla base per una notazione numerica possono benissimo essere introdotte a partire dal numero distributivo. Ma le idee di cardinalità e di ordinalità, che sono qui coimplicate, si ripresentano in un nuovo quadro concettuale. In realtà può accadere che si parli di decine o di dozzine restando tuttavia sul piano dei raggruppamenti senza che si affacci l’idea di una base per un sistema numerico. Affinché si possa parlare di una base è necessario che il «quanti per volta» assuma il carattere di una nuova grande unità e che le grandi unità si possano distinguere per livelli di ordine differenti. Dodici dozzine è una unità di secondo livello così come una dozzina è una unità di primo livello e gli elementi singoli di questa stratificazione potranno essere dunque considerate unità di livello 0. L’iterazione genera una stratificazione ordinata di livelli in rapporto alle «grandi unità». |6|
Queste sono considerazioni che riguardano il piano propriamente concettuale della questione. Ma queste considerazioni si sviluppano strettamente a ridosso del problema notazionale. Il concetto di numero nasce da una prassi. E questa prassi non potrebbe nemmeno cominciare ad essere esercitata se non si avvalesse di rappresentazioni. Questa istanza rappresentativa e i problemi ad essa collegati si fanno sentire già nel contare nel senso più lato e più lontano dalla serie aritmetica vera e propria e dal numero come costruzione logica. È interessante tuttavia notare che anche nei modi impropri del conteggio che terminano nel «molti» spesso si propongano forme gestuali di rappresentazione - cifre gestuali, per così dire - oppure parole di numero che presuppongono un raggruppamento. |7|
Presso un popolo dell’Oceania in cui il due si dice okasa, il quattro si dice okasa-okasa, il sei okasa-okasa-okasa. Poiché l’uno si dice urapun, come si dirà il tre e il cinque può essere lasciato indovinare al lettore. Ma giunti al 7 ed oltre, tutto è ras ovvero molti. |8|
Questo è un esempio molto interessante. Non sembrerebbe tuttavia opportuno parlare in casi come questi (e ve ne sono moltissimi) di sistemi con base due, per il fatto non vi è qui ancora una nozione pregnante del contare e tanto meno vi può essere una nozione propria della base[1]. |9|
Eppure questo dato storico-antropologico ha certamente interesse per la storia fenomenologico-ideale del numero. Affiorano infatti già qui due spunti fondamentali per la formazione dell’idea della base: le entità singole vengono raggruppate, il raggruppamento viene iterato in modo da dare luogo ad un metodo sistematico di costruzione dei nomi. I nomi dei numeri debbono essere prevedibili - il nome di un numero deve in certo modo esserci già prima che si sia mai manifestata un’occasione per il suo impiego. Oppure: il nome di un numero deve poter essere indovinato - come abbiamo fatto or ora. Entro certi limiti ciò accade nell’ultimo esempio, ma questi limiti sono limiti pratici e concettuali insieme - gli uni stanno, per così dire, dentro gli altri. |10|
La forma rappresentativa è ancora guidata dalla Gestalt percettiva della coppia e siamo ancora lontanissimi da una nozione autentica del contare; ed altrettanto lontani da una nozione vera e propria di base. |11|
Ciò che manca non è il raggruppamento come tale, ma il pensiero delle «grandi unità» ottenute per iterazione ricorsiva. |12|
Consideriamo più attentamente questo punto. Dobbiamo immaginare che il problema del raggruppare e di una notazione per il raggruppamento si sia posto ben presto nella storia del numero. Si tratta di un problema connesso all’impiego del numero, che a sua volta fa tutt’uno con l’impiego di una notazione per il numero. |13|
Prendendo le mosse dalla notazione-tratto, si potrà anzitutto ricorrere a segni per i raggruppamenti che saranno intesi come abbreviazioni dei segni-tratto corrispondenti. Ad una determinata molteplicità di tratti (ovvero di segni «1») si sostituisce un segno singolo speciale, facilmente riconoscibile, con chiaro vantaggio in rapporto alla perspicuità. I segni singoli potranno essere giustapposti esattamente come i tratti della notazione elementare. Per questo motivo si parla in generale di metodi notazionali di tipo additivo. Questi stessi segni potranno poi essere raggruppati e sostituiti con un segno singolo, e questo modo di procedere potrà essere ripetuto un certo numero di volte. Al di là di un certo limite tuttavia il segno numerico ridiventa percettivamente non dominabile. |14|
Ad esempio
11111 può essere sostituito con A
AA può essere sostituito con B
BBB può essere sostituito con C
Cosicché il numero 25 sarà rappresentato, ad esempio, da BBA. In questo tipo di metodo vi è una componente iterativa così come una tendenza alla gerarchizzazione, e dunque all’ordine. Questo metodo notazionale ha la caratteristica, verso il basso, di operare una differenziazione necessaria rompendo l’omogeneità «intrasparente» dei tratti, ma verso l’alto, esso opera una moltiplicazione dei segni che a sua volta non può che riproporre in altro modo una situazione di non perspicuità e di indominabilità. I segni via via nuovamente introdotti dal punto di vista della loro conformazione, seguono un principio di differenziazione qualitativa, quindi ancora un criterio puramente ghestaltico. |15|
Naturalmente le cose, dal punto di vista concettuale, non migliorebbero di molto se vi fosse coerenza nel raggruppamento, ad esempio scegliendo un unico «criterio» numerico del raggruppamento, e dunque qualcosa che assomiglierebbe ad una «base». |16|
Infine l’ordine e la disposizione dei segni non ha importanza. Il numero 25, a meno di speciali convenzioni aggiuntive, potrebbe essere espresso indifferentemente dai segni BBA, BAB, ABB. Il momento della gerarchizzazione, e quindi del livello di ordine dei raggruppamenti, è qui estraneo sia alla formazione del concetto che a quella del segno. I livelli non sono generati secondo la logica interna della concatenazione, ma si presentano in forma molto debole sulla base della circostanza ovvia che un’abbreviazione segnica presuppone che sia già stato introdotto il segno che viene abbreviato. Naturalmente sono possibili convenzioni restrittive o prescrizioni che impediscano o ostacolino la confusione. Vi saranno regole nella disposizione dei segni. Ad esempio, nella notazione romana il segno «I» cambia completamente di senso se viene messo a sinistra o a destra del segno «V». In generale i segni saranno letti in una unica direzione, da sinistra a destra o da destra verso sinistra. Ma queste convenzioni sono appunto soltanto convenzioni e non vi alcun rapporto di interdipendenza tra simili norme per le disposizioni segniche e il modo in cui si forma il concetto di numero. |17|
Il passaggio dalle notazioni additive a quelle posizionali non può perciò essere inteso soltanto come un passo avanti nella maneggevolezza e nella praticabilità. Esso è invece strettamente connesso con la riproposizione, ad un nuovo livello, della forma della concatenazione e della procedura ricorsiva che genera la serie aritmetica. |18|
Ciò che abbiamo chiamato prima «grande unità» è qualcosa di diverso da un raggruppamento e dalla giustapposizione additiva di raggruppamenti per il fatto che le grandi unità vengono prodotte all’interno di una procedura ricorsiva che ripete ad un livello più alto la procedura che genera la serie aritmetica rappresentata dalla notazione tratto. |19|
La prima novità importante che qui si introduce è che i segni non si moltiplicano «verso l’alto» in una proliferazione a piacere di configurazioni segniche differenti. Al contrario le unità di ordine superiore sono costituite dalle stesse cifre elementari. La percezione deve limitarsi ad effettuare il riconoscimento di queste cifre, ed a riferire l’ordine della loro disposizione presentato sul piano segnico alle differenze di livello delle unità sovraordinate. Esistono naturalmente ancora ampi margini per la convenzione, ma essa deve rispettare tutte le condizioni che fanno parte di una costruzione del segno che è diventata sempre più interna alla costruzione del concetto. |20|
Tanto interna che il tentativo di proporre l’intero problema sul piano della mera costruzione segnica potrebbe risultare molto istruttivo, come sintesi e conferma di ciò che stiamo sostenendo. Dovrebbe allora diventare chiaro non soltanto il sussistere di una rete di relazioni tra i vari tipi di numeri e le nozioni connesse (molteplicità, ordine, operazione, iteratività, distributività), ma anche il fatto che avremmo sempre in realtà a che fare con unità, benché di ordine superiore. |21|
Si consideri, per semplicità, un sistema a base binaria. Dovremo allora distinguere tra le cifre elementari o semplici, che saranno in questo caso due, e le cifre generate per composizione delle cifre semplici. Si noti che essendo due le cifre elementari, una di esse dovrà necessariamente designare l’unità, mentre l’altra cifra dovrà essere considerata equivalente nel suo senso a «nessuna unità». In altri termini una delle due cifre dovrà caratterizzare un posto vuoto [2] : da essa veniamo informati che nessuna unità occupa una certa posizione. Possiamo scegliere per entrambe le cifre una forma figurale qualunque, ma sarà ovvio optare per segni 1 e 0. La procedura di produzione dei segni potrebbe essere sintetizzata nel modo seguente:
Inizio 1x
Prima Regola x —> 0x
Seconda Regola x —> 1x
Vi sono qui due regole che debbono essere applicate l’una dopo l’altra nell’ordine in cui sono qui proposte per ciascun successivo elemento prodotto dalla procedura. L’applicazione delle regole genera dunque una coppia per ciascun elemento prodotto e una lista di coppie per ogni livello di iterazione. |22|
La prima base per l’applicazione della regola è naturalmente 1x che rappresenterà il livello zero. |23|
Di qui si trae, in forza della prima regola, 10x e, in forza della seconda regola, 11x. Questa coppia rappresenta il primo livello di iterazione e rappresenterà la base per una nuova applicazione delle due regole a ciascun elemento di essa e ottenendo per ogni segno una coppia di segni. |24|
Avremo dunque 100x, 101x, 110x, 111x - e questo risultato rappresenterà il secondo livello di iterazione. Il terzo livello di iterazione, ottenuto a partire da quest’ultimo esibirà la lista 1000x, 1001x, 1010x, 1011x, 1100x, 1101x, 1110x, 1111x, e così via. |25|
Per ciò che riguarda l’interpretazione in termini numerici dei segni così prodotti ci troviamo ancora una volta di fronte al rapporto tra ordine e numero di volte, in base al quale viene interpretata la posizione e dunque il «valore» da attribuire all’ «unità». |26|
Si riconsideri quanto detto or ora alla luce dello schema seguente, dove la x è stata soppressa, dal momento che essa rappresenta soltanto un artificio calcolistico interno alla procedura. Alla sinistra abbiamo segnalato il valore dell’unità ai vari livelli in termini di esponente - ma questo solo per rammentare la consueta formula matematica delle basi. Di fatto nello spirito della nostra esposizione, come non si effettuano addizioni sul piano della forma notazionale dei tratti, così non si effettuano operazioni di moltiplicazione o di elevazione alla potenza. Il problema invece è quello di un conteggio per grandi unità ottenute per ricorsione. L’attenzione deve essere richiamata sull’ordine e sulla ripetizione ricorsiva, che sono gli elementi fondamentali che si rispecchiano nella posizione della cifra elementare all’interno della cifra composta. |27|
| 1 | livello 0 | (20) |
| 10 11 | livello 1 | (21) |
| 100 101 110 111 | livello 2 | (22) |
| 1000 1001 1010 1011 1100 1101 1110 1111 | livello 3 | (23) |
Il segno 1 cambia di senso secondo il livello iterativo a cui appartiene, livello che è leggibile nella sua posizione. Il segno 0 indica a sua volta che non esistono unità nel livello iterativo indicato dalla sua posizione. Così la cifra 1011 verrà intesa nel modo seguente:
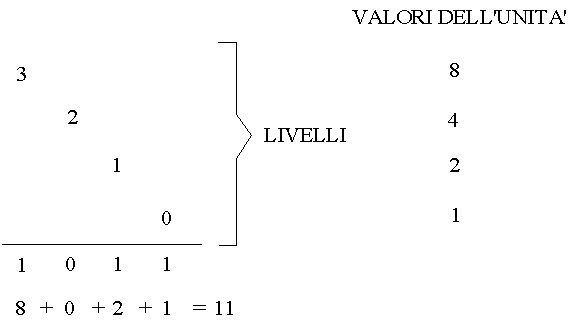
Possiamo anche presentare la derivazione dei segni attraverso una struttura ramificata come già fece a suo tempo Leibniz proprio in rapporto alla notazione binaria. |28|
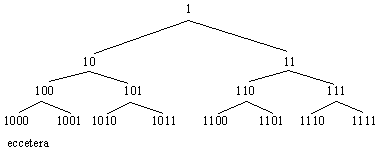
Nel caso del sistema decimale la procedura resta esattamente la stessa, come per ogni altra base. Aumenta solo, di poco, la complessità di questo nostro modo di presentare il problema[3].
Annotazione
È interessante ripetere le considerazioni precedenti dando ad esse la forma di una possibile procedura capace di generare i diversi sistemi numerici che si avvalga unicamente di regole di sostituzione per segni e della ripetizione della loro applicazione.
L’essenziale per la procedura di un sistema a pseudobase unaria è già stato detto.
Siano date una lista iniziale L1 formata dal segno x che abbiamo convenuto di utilizzare come segno per una sostituzione possibile ed un’ unica regola di sostituzione di x con 1x, il risultato che otteniamo alla prima applicazione sarà ovviamente 1x che aggiungeremo alla lista L1 ottenendo L1= {x, 1x}.
Da questa lista eliminiamo il primo elemento, quindi x, in modo che la seconda applicazione della regola di sostituzione possa avvenire sul risultato della prima applicazione. Otterremo dunque nella seconda applicazione la stringa 11x che verrà aggiunta alla lista L1; da questa verrà eliminato il primo elemento, e così via.
Nel linguaggio del noto programma Mathematica della Wolfram Research si avrebbero le seguenti righe di codice:
BaseUno[k_] :=
{
L1={"x"};
Do
[
{L1 = Append[L1, StringReplace[First[L1], {"x"->"1x"}]],
L1 = Drop[L1, 1], {k}
];
L1
};Scrivendo L1 nella penultima riga si stabilisce che L1 sia l’output a video della procedura.
Cosicché ad esempio l’istruzione:
BaseUno[4]
porrà in output 1111x (la x può naturalmente essere eliminata). Si noti che mentre k è un iteratore (il numero di volte in cui vengono applicate le regole e le istruzioni connesse), l’output è una pura e semplice stringa, quindi una mera costruzione grafica, che potrà ovviamente avere un’ interpretazione numerica.
La relativa complicazione con cui presentiamo ora la notazione-tratto ha le sue ragioni nel fatto che un sistema numerico di una base qualunque può essere prodotto esattamente nello stesso modo. Consideriamo nuovamente un sistema a base binaria.
La procedura per la produzione di cifre del sistema binario assumerebbe questa forma:
BaseDue[k_] :=
{
L1 ={"1x"};
Do
[
{L1 = Append[L1,StringReplace[First[L1], {"x"->"0x"}]],
L1 = Append[L1,StringReplace[First[L1],{"x"->"1x"}]],
L1=Drop[L1,1],}, {k}
];
L1
};Le regole di sostituzione sono ora due e debbono essere realizzate nell’ordine. Esse si applicano sempre al primo elemento di L1 e i risultati vengono aggiunti alla lista L1, alla quale, ad ogni iterazione, viene tolto il primo elemento. In breve ad ogni iterazione le ultime due cifre della lista sorgono dal risultato dell’applicazione ordinata delle regole alla prima cifra della lista L1.
È appena il caso di dire che per il sistema a base dieci avremo bisogno di dieci regole e che la lista L1 sarà inizialmente rappresentata dalla sequenza da 1 a 9. Per il resto il meccanismo di generazione delle cifre resta esattamente lo stesso.
BaseDieci [k_] :=
{
L1 ={"1x", "2x", "3x", "4x", "5x", "6x", "7x", "8x", "9x"};
Do
[
{L1 = Append[L1,StringReplace[First[L1], {"x"->"0x"}]],
L1 = Append[L1,StringReplace[First[L1],{"x"->"1x"}]],
L1 = Append[L1,StringReplace[First[L1], {"x"->"2x"}]],
L1 = Append[L1,StringReplace[First[L1],{"x"->"3x"}]],
L1 = Append[L1,StringReplace[First[L1], {"x"->"4x"}]],
L1 = Append[L1,StringReplace[First[L1],{"x"->"5x"}]],
L1 = Append[L1,StringReplace[First[L1], {"x"->"6x"}]],
L1 = Append[L1,StringReplace[First[L1],{"x"->"7x"}]],
L1 = Append[L1,StringReplace[First[L1], {"x"->"8x"}]],
L1 = Append[L1,StringReplace[First[L1],{"x"->"9x"}]],
L1=Drop[L1,1],}, {k}];
L1
};Ad ogni iterazione vengono ora prodotte dieci cifre attraverso l’applicazione delle dieci regole nell’ordine dato alla prima cifra di L1. Naturalmente L1 fa parte del «motore» della procedura, ma è invece secondario il fatto che proprio questa lista rappresenti l’output a video. È possibile, ad esempio, conservare in una lista L2 tutti i primi elementi che vengono via via eliminati da L1 ed in tal caso l’unione tra L2 e L1 ci darà nell’ordine, per ogni sistema, tutte le cifre prodotte ad una determinata iterazione. L’ultimo elemento di L2 potrà fornirci la stringa corrispondente all’iteratore, cosicché la procedura può anche essere utilizzata come una procedura di conversione dal sistema a base dieci ad altri sistemi.
L’interesse di tutto ciò non sta in questi possibili aggiustamenti e varianti, ma di generare come pure "cifre" i numeri di sistemi di una base qualsivoglia senza impiegare alcun calcolo aritmetico vero e proprio, ma unicamente attraverso la ripetizione ricorsiva di regole di sostituzione.
Note
|
|