4

- Sulla prima proposizione degli Elementi di Euclide
- In essa si formula un compito costruttivo
- Lo scopo della costruzione è tuttavia quello di mostrare le connessioni interne della figura
- Ogni passo della costruzione deve essere giustificato

Consideriamo la prima proposizione di Euclide - quella a partire dalla quale, dopo l'esposizione delle nozioni fondamentali, si delinea il grande progetto di una teoria deduttiva: ci troviamo di fronte non già ad una proposizione che enuncia uno stato di cose, il sussistere di una certa relazione o di una certa proprietà. |2|

In essa si formula un compito costruttivo, si pone un problema che sembra essere essenzialmente di realizzazione grafica:

Nella formulazione linguistica, dunque, non compare affatto una tesi relativamente ad una proprietà di un certo oggetto, ma un compito che deve essere portato a buon fine. |3|

La formulazione «come dovevasi dimostrare» che chiude le dimostrazioni nei nostri manuali elementari non è originaria di Euclide. La formula conclusiva euclidea corrisponde alla formulazione del compito, e dice dunque propriamente «come dovevasi fare». |4|

Nel momento in cui la geometria che è giunta ad un tale stadio di sviluppo da potersi proporre come una teoria in senso pregnante, come una teoria deduttiva, siamo anzitutto invitati a prendere carta e matita, riga e compasso ed a metterci al lavoro. Notato questo punto tuttavia, e non appena ci accingiamo alla costruzione che la proposizione ci propone, ci rendiamo conto di un'altra circostanza fondamentale che in realtà ci fornisce il senso autentico del compito proposto: la costruzione interessa in quanto essa è in grado di esibire dei passi internamente giustificati, cioè che hanno la loro giustificazione nelle connessioni interne della figura. Lo scopo è di mostrare queste connessioni e di mostrarle non già come dati di fatto rilevati nella mera osservazione della figura, ma come nessi determinati dal modo stesso in cui la figura è generata, e dunque come nessi appartenenti alla sua essenza. |5|

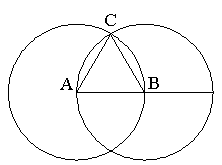
Consideriamo come procede la costruzione del triangolo sulla «retta terminata». Ci viene anzitutto richiesto di puntare alternativamente il compasso in A e in B e di realizzare due cerchi che si intersecheranno nel punto C. E poi di congiungere i punti A e B con il punto C. Si ottiene così il triangolo ABC.

Ora, ciò che importa sono le ragioni per le quali possiamo dire che abbiamo costruito un triangolo equilatero, non il dato di fatto della costruzione del triangolo equilatero. Alla costruzione è affidato unicamente il compito di esibire queste ragioni. |6|

Da un lato dunque è vero che l'impostazione del problema assume la forma di una costruzione, e questo rammenta l'origine dalla pratica con le figure. Dall'altro le componenti empirico-fattuali di questa pratica sono nettamente oltrepassate in una direzione di discorso essenzialmente diversa. |7|

Questo oltrepassamento è dimostrato soprattutto dal modo in cui si argomenta che, facendo così, il triangolo costruito è effettivamente equilatero. Esso è tale per via della eguaglianza dei raggi, di AB con AC e di AB con BC - e dunque anche di AC con BC. |8|

In realtà si potrebbero presentare le cose in tutt'altro modo. |9|

Il problema sia appunto quello di realizzare un triangolo equilatero su un segmento dato. Se vuoi realizzare questo compito devi fare così e così - devi puntare il compasso in A e poi in B. Devi congiungere poi il punto di intersezione C con A e con B. Facendo in questo modo otterrai un triangolo equilatero, come ti potrai convincere misurando i lati e constatando che essi sono eguali. |10|

Se presentassimo le cose in questo modo tutto si ridurrebbe ad una precettistica pratica e la conferma della bontà del risultato verrebbe poi da una constatazione empirica, dalla misurazione. Come se dicessimo: si è sempre fatto così, si è trovato che questo è un buon metodo ovvero che questa procedura ha sempre dato buoni risultati. |11|

Invece la prima proposizione non dice affatto questo, non ha affatto questo senso, né implicitamente né esplicitamente. L'esistenza di una relazione geometrica non trae conferma da una misurazione empirica, così come dal successo praticamente sperimentato di un metodo o di una procedura di costruzione. |12|

Ma da ciò segue che questa procedura non ha bisogno di essere concretamente realizzata: è sufficiente il pensiero della possibilità di una simile procedura e le conseguenze che io posso trarre da questo pensiero. Naturalmente una modificazione corrispondente subiscono le oggettività prodotte e gli enunciati su queste oggettività. Siamo appunto nel campo delle idealità. Più precisamente: stiamo cercando di spiegare che cosa significhi essere nel campo delle idealità. Fa indubbiamente parte di questa spiegazione il fatto che la costruzione non solo debba essere giustificata ad ogni suo passo, ma anche che la giustificazione debba essere trovata restando strettamemente all'interno degli Elementi. Poiché questa proposizione è appunto la prima, allora non potremo fare altro che richiamarci a tale scopo alle definizioni, ai postulati e alle nozioni comuni che fanno parte dell'apparato fondazionale della teoria. |13|

Rivediamo da questo punto di vista la realizzazione del compito enunciato dalla prima proposizione nei passi in cui essa può essere suddivisa. |14|

Il primo passo è quello di delineare il cerchio con centro in A e raggio AB. Il secondo passo consiste inversamente nel delineare il cerchio con centro in A e raggio BA. Ma questi due passi non sono affatto dati per compiuti e nulla più. Essi debbono invece essere giustificati, e proprio a questo scopo vi è un rimando anzitutto al Terzo Postulato, il quale afferma che possiamo sempre tracciare un cerchio con un raggio qualsiasi. |15|

Come terzo passo, si tracciano dal punto C, in cui i cerchi si intersecano, le linee congiungenti C con A e con B. E naturalmente anche questo passo deve essere giustificato - cioè deve essere giustificato il fatto che sia possibile tracciare quelle linee esattamente come nel caso precedente dei cerchi. Il rimando è qui al Primo postulato: È sempre possibile tracciare una linea da un qualsiasi punto ad ogni altro punto[1]. |16|

Abbiamo infine - non tanto un quarto passo - quanto una considerazione conclusiva che deve effettuare il passaggio alla formula «come dovevasi fare». Si tratta di confermare che il triangolo costruito nei passi precedenti è effettivamente un triangolo equilatero, e per questo forniamo una giustificazione intrinseca che può essere tratta dal peculiare metodo di costruzione del triangolo stesso. Si sono tracciati dei cerchi: e la ragione della equilateralità sta nella Definizione XV che riguarda l'eguaglianza dei raggi come condizione definitoria del cerchio; e nella Prima nozione comune che riguarda la transitività dell'eguaglianza e che rende possibile l'impiego di questa condizione in rapporto al problema proposto. Del resto, non è affatto ovvio accingersi a disegnare un triangolo tracciando cerchi! |17|

§ 3

§ 5