Numero e figura
Idee per un’epistemologia della ripetizione
|
II, § 9
|
Giovanni Piana
|
9
- Variazioni sul tema del pentagramma pitagorico e scoperta dell’algoritmo che lo genera
Come si sarà ben compreso, non siamo affatto disposti a considerare il linguaggio or ora introdotto come un puro artificio informatico, privo di elementi che invitino alla riflessione teorica. Esso è certamente uno strumento assai utile, è un traccialinee - anzi, come subito vedremo - uno stupefacente traccialinee, nello stesso senso in cui lo sono la riga e il compasso euclideo, i quali sono strumenti materialmente determinati, con caratteristiche dovute alla loro consistenza materiale, pronti tuttavia a dissolversi come contraccolpo rispetto ai sensi ideali da cui vengono investiti gli oggetti da essi prodotti. |1|
Precisato questo punto possiamo dar libero corso alle nostre passioni di fenomenologi interessati alle strutture lasciando che il nostro traccialinee manifesti pienamente quella capacità di produrre immagini che abbiamo finora appena intravista. |2|
Intanto vogliamo svolgere una sorta di esercitazione ricollegandoci al pentagramma dei pitagorici. Per impratichirci del nostro strumento quale esercizio potrebbe essere migliore del tentativo di stabilire la formula di questa figura, lo schema operativo che rappresenta la sua essenza! |3|
Oltretutto nessuno, che io sappia, lo ha mai fatto, e questo può servirci da stimolo - così come la stessa idea di possedere la cifra informatica di una figura tanto antica e veneranda. |4|
Questa ricerca può essere affrontata, come tutte le cose di questo mondo, in modo prudente e riflessivo, avviandoci con calma verso una determinata direzione con le certezze di un ragionamento convincente fatto in precedenza; oppure in modo imprudente e irriflessivo, sperimentando un poco alla cieca, azzardando questo «assioma» o quella regola, cercando di rendersi conto, alquanto all’ingrosso, di che cosa accada. Naturalmente la via migliore è la prima. Ma come resistere alla tentazione di qualche prima prova, guidati alla meglio dal fatto che in ogni caso in questa figura c’è un pentagono, e vi sono i diametri che formano una stella ed eventualmente i triangoli formati dall’intreccio delle figure? Uno dei molti nomi con i quali i Pitagorici chiamavano questa figura era quello di 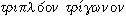 , cioè di triplo triangolo. In effetti possiamo anche vedere in essa la sovrapposizione di tre triangoli eguali. L’idea dunque - molto sommaria, molto azzardata e non particolarmente riflessiva, è quella di provare a far giocare insieme, nello schema operazionale, intanto pentagono e stella. Sappiamo già che il pentagono è rappresentato simbolicamente da «F-F-F-F-F» con l’angolo a 72°: |5|
, cioè di triplo triangolo. In effetti possiamo anche vedere in essa la sovrapposizione di tre triangoli eguali. L’idea dunque - molto sommaria, molto azzardata e non particolarmente riflessiva, è quella di provare a far giocare insieme, nello schema operazionale, intanto pentagono e stella. Sappiamo già che il pentagono è rappresentato simbolicamente da «F-F-F-F-F» con l’angolo a 72°: |5|
La stella ci riserva subito una piccola sorpresa dal momento che essa risulterà «F--F--F--F--F» : ciò significa che la differenza rispetto al pentagono sta unicamente nella grandezza della deviazione dalla direzione rettilinea, che è doppia rispetto al pentagono. La formula è dunque essere esattamente la stessa di quella del pentagono, con la sola differenza dell’angolo portato a 144°.

Siamo subito avvertiti dal simbolismo, e precisamente dal simbolismo non ancora interpretato, di essere alla presenza di costruzioni strettamente solidali. |6|
Ed ecco alcuni risultati. Naturalmente ci basta enunciare lo schema operazionale: il programma di calcolo realizzerà la figura corrispondente alla stringa ottenuta dopo un certo numero di iterazioni. |7|
Di qui in avanti per pure ragioni di chiarezza daremo una numerazione progressiva agli schemi operazionali ed alle figure ottenute, indicando tra parentesi quadre il numero di iterazioni corrispondenti. |8|
Con prima iterazione si intenderà la prima applicazione delle regole all’assioma, con seconda iterazione l’ulteriore applicazione delle regole al risultato precedentemente ottenuto, e così via. Nel caso che ciò sia opportuno verrà indicato all’inizio anche la condizione angolare, che ora viene omessa essendo sempre pari a 72°. |9|
|
Schema operazionale n. 1
|
|
Assioma |
Regole |
|
F--F--F--F--F |
F ->F-F-FA
A-> F-F-F-F-F |

fig. 1, I
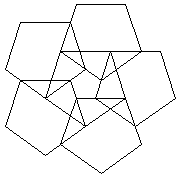
fig. 2, II
|
Schema operazionale n. 2
|
|
Assioma |
Regole |
|
F--F--F--F--F |
F-> F-F-FA
A->F--F--F--F--F |

fig. 3, III
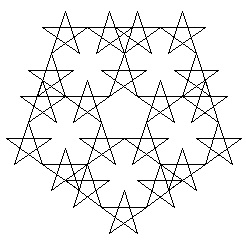
fig. 4, III
|
Schema operazionale n. 3
|
|
Assioma |
Regole |
|
F--F--F--F--F |
F-> F+F+FA
A-> F--F--F--F--F
|
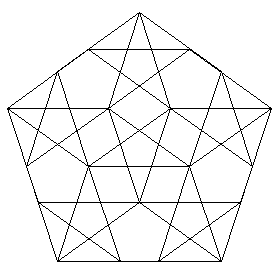
fig. 5, II
Il traccialinee ha cominciato a funzionare - l’algoritmo elabora le sostituzioni ed ai primi passi mostra ovunque come l’una figura si costruisca sull’altra, dentro l’altra, insieme all’altra. Stelle e pentagoni si alternano qui in maniera sorprendente sotto i nostri occhi. La stella scompare nella fig. 2 dove vi sono cinque pentagoni eguali e cinque triangoli eguali, che nella loro sovrapposizione danno luogo ad un pentagono centrale più piccolo.
Una piccola modificazione all’interno del simbolismo mostra nella fig. 3 come cinque stelle, ognuna delle quali contiene nel suo interno un pentagono, possano formare un pentagono con un lato eguale a quello della stella formando un nuovo pentagono, i cui lati sono suddivisi dai vertici del pentagono inscritto esattamente in due parti eguali, ciascuna delle quali rappresenta a sua volta la sezione aurea del lato della stella.
Con una ulteriore iterazione l’algoritmo produce la fig. 4, in cui tutti i pentagoni appaiono costruiti attraverso figure stellate - almeno considerandoli nel modo in cui si presentano alla vista. Occorre infatti richiamare l’attenzione sul fatto che, ovviamente, non solo non possiamo di norma «intuire» dallo schema operazionale che cosa accadrà nell’interpretazione figurale, ma anche che la visione della figura non è affatto in grado di informarci sul modo in cui è stata costruita, dal momento che in essa non vi è alcuna «memoria» del percorso che è stato seguito, e sono tra l’altro possibili anche sovrapposizioni di tragitti. Le nostre stesse descrizioni guardano alla forma visibile della figura, e non al processo costruttivo come tale.
Una piccola modificazione della regola per F (il «+» che sostituisce il «-») produce, alla seconda iterazione, la fig. 5, dove all’interno di un pentagono vengono tracciate cinque stelle che formano con i loro lati cinque pentagoni; inoltre i lati delle cinque stelle formano un pentagono centrale che contiene una stella.
Nello stesso tempo si noti che la sequenza del pentagono «F-F-F-F-F» compare solo nel primo schema opeprazionale, mentre negli altri abbiamo a che fare soltanto con la sequenza della stella e la sequenza di tre F. Ciò che prima dicevamo in rapporto alla figura - che vi è un modo di considerarla per cui essa invita alla trasformazione - sembra ora si possa dire in rapporto al simbolismo concepito come produttivo di figure. Un calcolo ne suggerisce un altro, e si tende a procedere di variante in variante muovendosi all’interno di una famiglia di calcoli nella quale l’uno è quasi una ripetizione dell’altro. Vogliamo procedere con gli esempi.
|
Schema operazionale n. 4
|
|
Assioma |
Regola |
|
-F--F--F--F--F- |
F-> F+F+F |
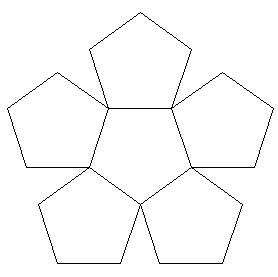
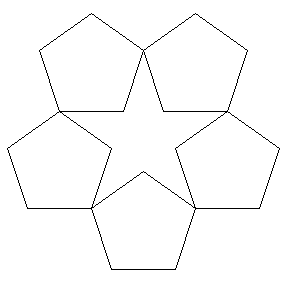 fig. 6, II fig. 7, III
fig. 6, II fig. 7, III

fig. 8, IV

fig. 9, V
Ciò che rende singolare questa sequenza è il fatto stesso che le figure siano successivamente generate dallo stesso algoritmo e che in essa si proponga, sarei tentato di dire, con ostentazione, la relazione di struttura tra il pentagono e la stella. Il pentagono della fig. 6 appare «riempito» alla seconda iterazione dello schema seguente:
|
Schema operazionale n. 5
|
|
Assioma |
Regole |
|
F--F--F--F--F |
F-> AF-F-FA
A -> F--F--F--F--F |
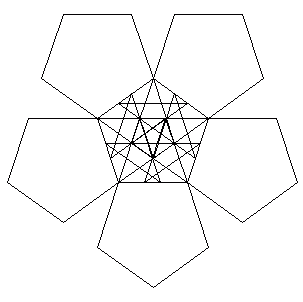
fig. 10, II
Dallo stesso algoritmo si sviluppa in terza iterazione la seguente figura che ha un pentagono stellato anche nel suo punto centrale più interno:
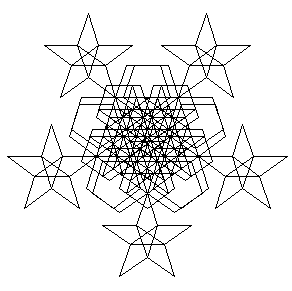
fig. 11, III
La stella al centro la si può vedere naturalmente soltanto ingrandendo il dettaglio:
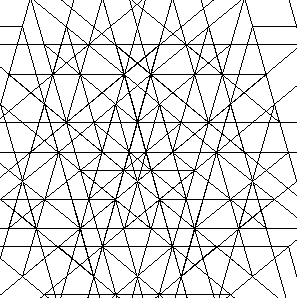
Inseguendo queste variazioni sul tema ci siamo tuttavia allontanati dal problema da cui avevamo preso le mosse al punto da averlo quasi perduto di vista. Fin qui ci ci siamo aggirati tra stelle e pentagoni continuamente rinascenti che ricompaiono in contesti sempre diversi. Ma la nostra ambizione era quello di trovare una formula per la generazione del pentagramma pitagorico, il suo schema costruttivo. Ciò significa che non ci basta vedere affiorare qui e là, all’interno delle configurazioni più varie, la tipica configurazione della stella dentro il pentagono o del pentagono dentro la stella. Il nostro scopo iniziale era invece quello di ottenere un algoritmo in cui quella configurazione si genera l’una dentro l’altra ad ogni iterazione successiva.
In realtà non possiamo sperare di venire a capo di esso se evitiamo una riflessione preliminare che suggerisca la direzione in cui cercare questa formula. Anzitutto il lato della stella che è diagonale del pentagono circoscritto va progressivamente riducendosi e di conseguenza dobbiamo preordinare nell’algoritmo una simile riduzione. Uno dei vantaggi dei linguaggi L-systems in genere è quello di poter aggiungere regole e istruzioni senza nessuna restrizione. Si tratta semplicemente di introdurre un altro segno e una regola per la sua interpretazione quando verrà incontrato nella lista finale. Ad esempio siamo liberi di introdurre un segno R che venga interpretato come un’istruzione di riduzione della lunghezza del tratto F.
Per ciò che riguarda la grandezza della riduzione dobbiamo analizzare meglio la figura. Essa chiama in causa una relazione che possiamo supporre fosse nota ai pitagorici almeno dal punto di vista «figurale» e che comunque fa parte degli albori della scoperta dei numeri irrazionali : ogni lato d della stella viene suddiviso nei punti di intersezione con gli altri lati secondo il rapporto di sezione aurea; e precisamente in modo tale che ogni lato d della stella risulta suddiviso in tre parti a, b, c tali che a+b=c+b = sezione aurea (media ragione) di d, essendo b il lato del pentagono interno. Il lato della stella deve ridursi esattamente della sua sezione aurea, cioè deve diventare eguale alla sua «estrema ragione» (c) essendo il lato della stella interna eguale all’«estrema ragione» del lato della stella esterna. Ponendo a 1 la lunghezza del lato della stella, la sezione aurea calcolata nei suoi primi cinque decimali sarà pari a 0.61803, e il valore ricercato sarà 1 - 0.61803 = 0.38197. Quest’ultimo valore farà dunque parte della regola per R come una costante per la quale va moltiplicata la lunghezza di F. L’algoritmo prevederà dunque, che incontrando il segno R, venga eseguita questa operazione aritmetica che serve al ricalcolo del valore della lunghezza di F: il segno R ha perciò, all’interno del simbolismo, una funzione del tutto diversa dal segno F ed anche dai segni di mera sostituzione intralinguistica.
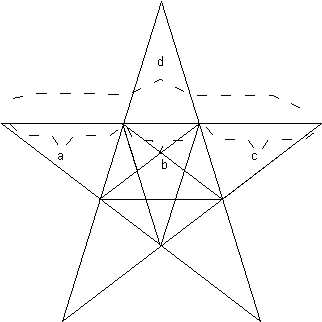
Oltre al segno R abbiamo bisogno di un altro segno, sia«!» e di una regola per esso. In base a tale regola esso verrà interpretato come un segno a partire dal quale il significato del segni «+» e «-» dovrà essere scambiato. A differenza del precedente, quest’ultimo segno appartiene allo standard dei linguaggi L-systems.
Fatte queste considerazioni possiamo proporre il seguente schema operazionale che rappresenta lo schema secondo il quale può essere ricorsivamente costruito il pentagramma pitagorico. In esso non vengono ulteriormente specificate le funzioni di «R» e di«!»[1].
|
Schema operazionale n. 6
|
|
Assioma |
Regola |
|
x |
x->F--F--F--F--F--RF-!x |
La punta del nostro ipotetico traccialinee comincia a disegnare la figura da sinistra a destra cominciando dal punto I1; dopo la prima applicazione della regola essa si troverà esattamente nel punto I2, come ciascuno potrà del resto verificare con carta e matita. Alla seconda e terza iterazione si otterranno le stelle annidate l’una dentro l’altra, nel pentagono interno. In via di principio la procedura è iterabile essendo l’iterabilità assicurata dal carattere ricorsivo della regola per «x».
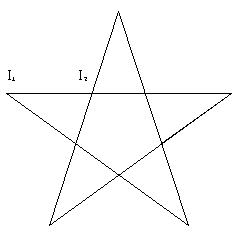
fig. 12, I

fig. 13, II
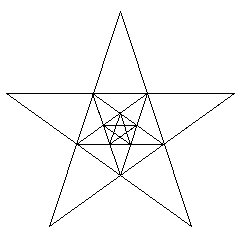
fig. 14, III
eccetera
La forma pentagonale non compare nella formula ed è sempre un risultato del tracciamento della stella, come del resto accadeva per lo più nei nostri esempi precedenti. Questo è un piccolo dettaglio, ma che assume per noi un particolare significato proprio in rapporto al problema della forma-figura. Abbiamo rammentato all’inizio l’idea della forma come contorno, riferendola all’idea della cosa. In rapporto a questa idea della forma è certo più naturale dare maggiore importanza al pentagono, considerando la stella piuttosto come una formazione interna che sorge come risultato del tracciamento delle diagonali del pentagono. Volendo poi parlare delle forme che ne risultano, si presterà attenzione ad una partizione in triangoli e pentagono oppure ai tre triangoli sovrapposti. La descrizione che potremmo dare della stella potrebbe dunque essere quella di un intero fatto di determinate parti che hanno il carattere di parti-figure, ad esempio potremmo dire che si tratta di un pentagono sui lati del quale sono costruiti cinque triangoli. All’inizio anche noi abbiamo dato una descrizione della figura in questi termini. D’altra parte il concetto eminente di poligono non è certo dato, nella geometria elementare, dai poligoni intrecciati a cui la stella appartiene. Ma il modo di intendere la figura è cambiato: essa sorge da un percorso, essa è propriamente un tracciato e la sua unità è data dall’unità del tracciato.
Adottando questo punto di vista il pentagono e non la stella ha carattere di risultato e la stella non è ottenuta dalla suddivisione di un pentagono. Così doveva essere anche per i Pitagorici: è molto probabile infatti che, proprio come si fa nell’algoritmo generatore, il gesto da cui sorgeva la figura fosse appunto quello di realizzare un tracciato che si ricongiungeva al punto di partenza in un percorso ininterrotto nel quale veniva disegnata anzitutto la stella, quindi veniva raggiunto il vertice del pentagono interno sovrapponendosi ad un breve tratto già tracciato, e da quel vertice, sempre senza interruzioni, poteva iniziare la realizzazione di una nuova stella.
Questo gesto è poi quello che ci dà la chiave per trovare l’algoritmo generatore - che proprio per questo non rappresenta davvero, da parte nostra, una grossa scoperta! L’algoritmo non fa altro che ripercorrere l’itinerario di quel gesto: cominciando dal vertice a sinistra viene tracciata la stella e poi, dopo aver riguadagnato questo vertice, il tratto viene ridotto nella misura voluta in modo da ripercorrere il tratto già tracciato fino al vertice del pentagono interno, e qui si apre il nuovo ciclo, esattamente identico al precedente.
Annotazione
Proprio per il fatto che spesso gli storici della matematica passano sotto silenzio questo punto o non dànno ad esso il rilievo che merita, è opportuno richiamare l’attenzione sui molti indizi che rivelano un interesse dominante per le procedure ricorsive da parte pitagorica - e già nel pitagorismo antico. Una corrente filosofica che assume a proprio emblema un simile pentagramma era certamente consapevole delle meraviglie contenute nella sua struttura, e dunque della «logica» interna alla figura. Questo aspetto è in ogni caso illustrato soprattutto dalla teoria dei «numeri figurati». In rapporto ad essi viene ancora in mente la domanda di Wittgenstein se l’aritmetica non possa essere intesa come una sorta di geometria. E la problematica di cui essi sono portatori si presenta molto seducente per chi sia interessato, come noi siamo, al numero ed alla figura sotto il profilo del problema della ripetizione. Nei numeri figurati non si deve tuttavia cogliere una rozza geometrizzazione che «mal si accorda - come osserva Michel - alle nostre abitudini attuali» e che saremmo facilmente portati a ritenere «aberrante», bensì ci si deve rendere conto che, secondo la prospettiva pitagorica, «a ciascun numero corrisponde una figura visibile che non è un segno convenzionale come sarebbe una cifra, ma un riflesso della sua essenza. La figura traduce le proprietà del numero. Inversamente le proprietà dei numeri possono essere colte attraverso quelle delle figure; ma dobbiamo ricordarci che è dal numero che prendiamo le mosse» (P. H. Michel, De Pythagore a Euclide, Paris 1950, p. 296). Nella nostra terminologia e in conformità alla nostra trattazione, noi diremmo piuttosto che il numero figurato può essere considerato come un metodo di notazione aritmetica a struttura ricorsiva, impiegato per generare seriazioni, e quindi per operare «concettualizzazioni» sulla base di schemi operazionali e per evidenziare in questo modo varie forme di rapporti tra tipi di numeri.
Note
[1] È appena ovvio notare che non abbiamo qui preoccupazioni di «buona forma», che richiederebbe una digresssione sugli L-systems non necessaria per i nostri scopi, ma piuttosto di chiara comprensione da parte del lettore. In ogni caso nel programma informatico compariranno, come parametri, l’assioma e la regola così formulata, e non le regole per «!» o per «R» che verranno scritte invece motore del programma stesso. Per questa ragione vengono trascurate nel nostro schema operazionale n. 6.
Indice
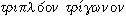 , cioè di triplo triangolo. In effetti possiamo anche vedere in essa la sovrapposizione di tre triangoli eguali. L’idea dunque - molto sommaria, molto azzardata e non particolarmente riflessiva, è quella di provare a far giocare insieme, nello schema operazionale, intanto pentagono e stella. Sappiamo già che il pentagono è rappresentato simbolicamente da «F-F-F-F-F» con l’angolo a 72°: |5|
, cioè di triplo triangolo. In effetti possiamo anche vedere in essa la sovrapposizione di tre triangoli eguali. L’idea dunque - molto sommaria, molto azzardata e non particolarmente riflessiva, è quella di provare a far giocare insieme, nello schema operazionale, intanto pentagono e stella. Sappiamo già che il pentagono è rappresentato simbolicamente da «F-F-F-F-F» con l’angolo a 72°: |5|
















