
|
Idee per un’epistemologia della ripetizione |
|
Giovanni Piana
|
10
- Variazioni sul tema della curva di Koch
- Problemi attinenti al rapporto tra figura generata e algoritmo generatore
|
Schema operazionale n. 7 |
||
|
Assioma |
Regola |
Condizione |
|
F |
F->F+F--F+F |
Angolo = 60° |
Figuralmente l’assioma è dunque rappresentato dal tratto unitario di base. |1|

La parte a destra della freccia della regola dalla figura seguente:

Ciò significa che ogni tratto F delle figure via via generate sarà sostituito da quest’ultima configurazione. |2|
Lo svilupppo dell’algoritmo potrebbe essere presentato come uno schema ad albero nel modo seguente:

Si noti che potremmo assumere come assioma la regola stessa, senza modificazioni significative se non ovviamente il fatto che la nostra figura iniziale sarà rappresentata dalla configurazione precedente piuttosto che dalla linea. Con ciò si mostrerebbe già in azione nel simbolismo il tema dell’autosimilarità. Infatti ciò che colpisce nel simbolismo seguente
|
Schema operazionale n. 8 |
||
|
Assioma |
Regola |
Condizione |
|
F+F--F+F |
F->F+F--F+F |
Angolo = 60° |
è anzitutto il fatto che ogni F dell’assioma venga sostituito con una configurazione di F che è eguale all’assioma stesso. Abbiamo dunque qui un caso piuttosto differente rispetto a quello del pentagramma pitagorico. Di ogni tratto corrispondente ad F sembra perfettamente pertinente affermare che si tratta di una parte dell’intero figurale corrispondente a «F+F--F+F». Questa parte tuttavia è a sua volta costituita di parti ognuna delle quali ha esattamente la stessa configurazione dell’intero. Potremmo anche dire che ogni parte è eguale, a meno della variazione di scala, alla parte immediatamente sovraordinata che rappresenta il suo intero relativo. La nozione di autosimilarità è qui esemplificata secondo un’accezione ad un tempo molto precisa e molto forte.|3|
Applicando iteratamente le regole dello schema operazionale n. 7 otteniamo la notissima sequenza delle figure:

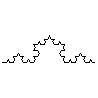

È difficile reagire alla tentazione di fare, anche in questo caso, almeno qualche passo nel seguire le metamorfosi delle forme attraverso le variazioni possibili dell’algoritmo, senza molto riflettere sullo scopo. D’altra parte si tratta di un gioco che, oltre ad esibire le capacità della ripetizione, potrebbe forse suggerire l’idea di un’indagine sistematica che metta a capo ad una tipologia di questi calcoli, attenta anche agli aspetti fenomenologico-figurali ed alla relazione tra questi aspetti e la loro struttura. Potrebbe essere interessante prendere in esame la possibilità di individuare tipi di calcoli con caratteristiche diverse, nei loro nessi con le forme figurali, e dunque i tipi di metamorfosi indotte da determinate variazioni all’interno del simbolismo. |4|
Ecco che cosa può risultare con formule simili a quelle della curva di Koch o almeno non particolarmente più complesse di essa. |5|
|
Schema operazionale n. 9 |
||
|
Assioma |
Regola |
Condizione |
|
F |
F->-F+F--F+F- |
angolo = 60° |
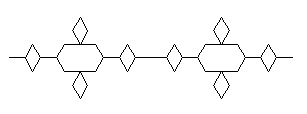
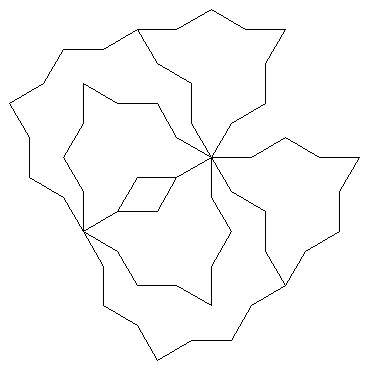
fig. 20, III

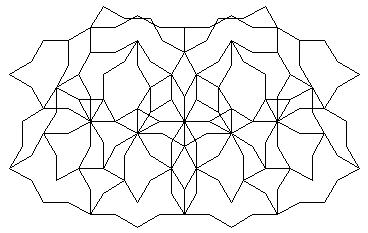
fig. 21, IV
|
Schema operazionale n. 10 |
||
|
Assioma |
Regola |
Condizione |
|
F+F--F+F |
F->-F+F--F+F- |
angolo = 30° |
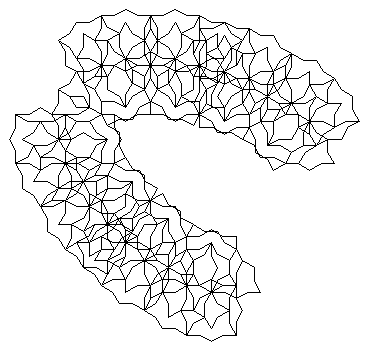
Nello schema seguente compare, oltre a "!" già rammentata in precedenza, un’altra istruzione standard dei linguaggi L-systems, l’istruzione indicata l’istruzione indicata da «|» che realizza l’inversione della direzione di movimento della linea. |6|
|
Schema operazionale n. 11 |
||
|
Assioma |
Regole |
Condizione |
|
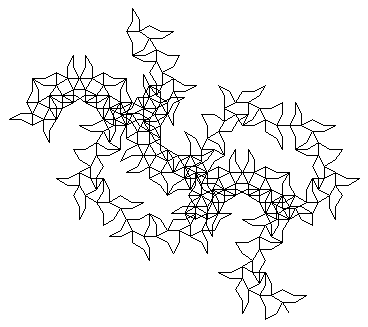
FFF |
F -> !F+F--F+F| |
angolo = 30° |
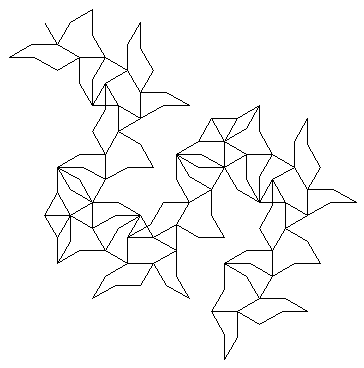
|
Schema operazionale n. 12 |
||
|
Assioma |
Regola |
Condizione |
|
FA |
|
angolo = 30° |
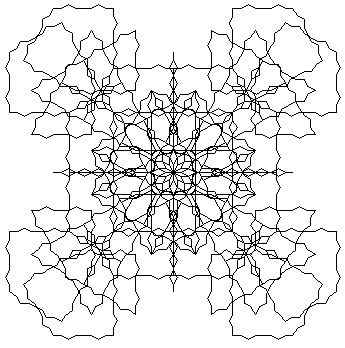
L’aspetto «decorativo» o «ornamentale» che compare spesso in queste figure risulta naturalmente dalle scelte effettuate nella struttura dell’algoritmo, ed in particolare è una conseguenza della scelta dell’angolo e dell’esistenza di particolari simmetrie all’interno dello schema operativo, che si vanno complicando ed intrecciando di iterazione in iterazione, arrivando a livelli di complessità strutturale che sarebbero davvero inimmaginabili senza l’aiuto di un automatismo capace non soltanto di generare la stringa, ma anche di fornire l’interpretazione grafica. Si consideri in particolare l’ultima «meraviglia» (fig. 27) che mi è accaduto di «scoprire» peregrinando tra i calcoli. |7|
Da essa prendiamo il ritaglio della sua zona centrale, per mostrare la complessità che risulta dal meccanismo iterativo di un algoritmo tanto semplice. |8|
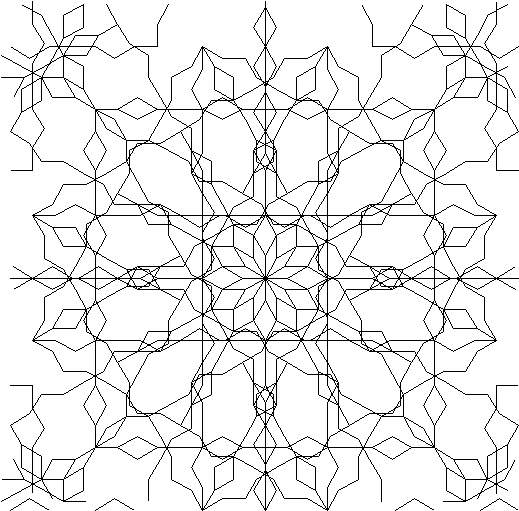
In questo ritaglio si possono vedere - oltre lo schema elementare della regola dell’algoritmo di Koch, che è onnipresente nelle nostre variazioni - un intreccio di figure geometriche note, ad esempio due quadrati di cui l’uno sovrapposto all’altro secondo una certa inclinazione, un esagono, un ottagono, ed altro ancora: ad esempio, ognuno dei due quadrati può essere considerato suddiviso in nove quadrati. Numerosi piccoli parallelogrammi sono, per così dire, ovunque ordinatamente distribuiti - si tratta in realtà di due schemi elementari sovrapposti. |9|
A proposito di una descrizione come questa, che presta attenzione agli aspetti figurali, così come si offrono direttamente alla percezione, occorre tuttavia riprendere alcune osservazioni che sono già state anticipate in precedenza e che riguardano il rapporto tra lo schema operazionale e il risultato figurale. |10|
Si è già in effetti fatto notare che di norma lo schema operazionale non lascia certo facilmente intravvedere il risultato grafico. Al più può accadere in taluni casi interessanti di cogliere un nesso tra risultato grafico e schema operazionale. Prendiamo ad esempio un assioma di forma «XYYX»; vi è qui una articolazione secondo la quale questa stringa si lascia suddividere in due parti, delle quali l’una è l’inverso dell’altra. |11|
Si consideri ora il seguente schema operazionale nel quale oltre la simmetria dell’assioma, si presentano ulteriori simmetrie nelle regole per X e per Y (lettere che peraltro qui compaiono come elementi «intralinguistici»):
|
Schema operazionale n. 13 |
||
|
Assioma |
Regola |
Condizione |
|
XYYX |
|
angolo = 30° |
Facendo agire questo schema operazionale otteniamo le seguenti figure:
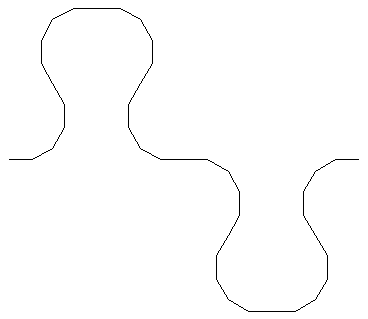
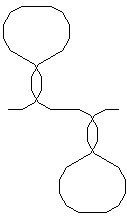
Non c’è dubbio che tra la figura risultante e lo schema operazionale, nel suo gioco di inversioni e di simmetrie, presenti sia negli assiomi che nelle regole, sussista un nesso che può anche manifestarsi nel confronto tra la figura e lo schema. Ma anche in questi casi occorre mantenere una distinzione assolutamente necessaria tra il modo della costruzione e l’interpretazione percettiva del suo risultato. |12|
Ad esempio, tenderemo a considerare la figura che segue

come un rettangolo tagliato da un linea retta. Io penso che chiunque fosse richiesto di copiare questa figura traccerebbe anzitutto il rettangolo e poi la linea retta. Invece l’algoritmo ha prodotto questo risultato in modo interamente diverso che diventa visibile non appena spostiamo l’angolo di qualche grado, ad esempio da 90 a 87. Ora la figura tracciata mostra il modo effettivo della sua costruzione.
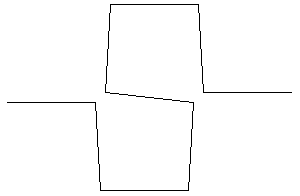
Analogamente nella figura seguente si stenterà a vedere lo stesso modulo figurale ripetuto quattro volte:
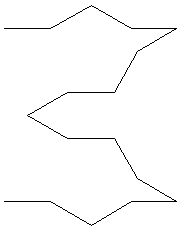
L’attenzione sarà invece attratta soprattutto dalle due punte sulla destra, oltre che dalla simmetria che si viene a creare sull’asse orizzontale; inoltre la figura mantiene un singolare carattere di incompletezza, dovuta forse proprio al fatto che la simmetria sull’asse orizzontale non è accompagnata da una simmetria sull’asse verticale. Come accade invece nel caso seguente:
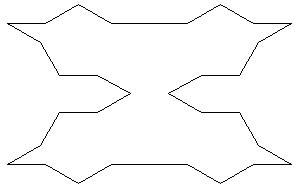
Il risultato figurale è dunque, nel suo modo di apparire, del tutto autonomo rispetto allo schema operativo che lo genera. Una conseguenza di ciò è che, nonostante il fatto che queste costruzioni siano governate dal determinismo più rigoroso a meno non inseriamo noi stessi elementi di casualità nelle regole (cosa perfettamente possibile), la presenza della ripetizione può rimanere nascosta. Le figurazioni generate ci possono apparire fortemente irregolari, senza un piano e persino caotiche. È interessante notare che le figurazioni considerate nella loro successione non sempre e non necessariamente appaiono concatenate tra loro: ciascuna di esse occupa una posizione ben determinata all’interno di una serie, in quanto esse sono subordinate ad un unico schema formale, e sono dunque «specie dello stesso genere»: e tuttavia questa subordinazione ad un unico schema formale è tavolta compatibile con la massima differenza fenomenologica tra un risultato e il risultato ad esso immediatamente successivo. Inoltre, una piccola modificazione dell’algoritmo o di una sua condizione, talvolta genera una piccola distorsione nella figura, talora una modificazione «catastrofica». |14|
|
|